P15163 [SWERC 2022] Crossing the Railways

Isona 在一个火车站里。这个车站有两个站台，它们之间有 $m$ 条平行的铁路，可以看作无限长的直线。每条铁路用一个从 $1$ 到 $m$ 的整数标识，铁路 $1$ 最靠近第一个站台，铁路 $m$ 最远。相邻铁路之间相距 $1$ 米，每个站台与其最近的铁路也相距 $1$ 米。 Isona 正站在第一个站台的内侧边缘，这时她意识到自己忘了验票！第二个站台上有一个验票机，恰好在她当前位置的正对面（因此，Isona 与验票机的距离是 $m + 1$ 米）。只剩下 $s$ 秒来验票，而指定用来穿过铁路的天桥离验票机太远了。因此，Isona（她非常勇敢且有点粗心）将沿着垂直于铁路本身的直线跑过去穿越铁路。Isona 只能向前跑（不能后退），也可以静止不动。当她以最大速度奔跑时，她需要 $v$ 秒来穿越 $1$ 米。她可以以小于或等于最大速度的任何速度奔跑。 只有一个问题：有 $n$ 列火车计划通过这些铁路。第 $i$ 列火车将使用铁路 $r_i$。它将在从现在起的 $a_i$ 秒开始穿越 Isona 与验票机之间的直线，并在 $b_i$ 秒结束。当然，Isona 不能在火车通过时穿越一条铁路。形式化地说，对于每个 $i = 1, \, 2, \, \dots, \, n$，Isona 不允许在任何满足 $a_i < t < b_i$ 的时间 $t$ 处于铁路 $r_i$ 上（但她可以在 $a_i$ 或 $b_i$ 时刻穿越）。 下图概括了这种情况。图中有 $m = 4$ 条铁路，可以看到两列火车；正在通过铁路 $3$ 的火车当前正在穿越 Isona 与验票机之间的直线。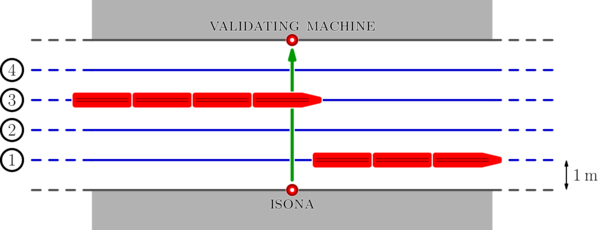 :::align{center}  ::: Isona 是一个非常优秀的跑步者，但每次她不得不改变奔跑速度时都会感到疲劳。为了在从现在起的 $s$ 秒内到达对面站台的验票机，她需要执行的最少速度变化次数是多少？注意开始时 Isona 没有在跑。她可以在任何时间开始跑。她开始跑的瞬间（即速度变为正时）不计为速度变化。

输入的第一行包含四个整数 $n$、$m$、$s$、$v$（$1 \leq n \leq 500$，$1 \leq m \leq 10$，$1 \leq s, v \leq 10^9$）—— 分别表示火车的数量、铁路的数量、Isona 可以花费在穿越铁路上的最长时间（秒），以及她以最大速度穿越 $1$ 米所需的秒数。 接下来的 $n$ 行每行包含三个整数 $a_i$、$b_i$、$r_i$（$1 \leq a_i < b_i \leq 10^9$，$1 \leq r_i \leq m$）—— 第 $i$ 列火车开始和结束穿越 Isona 与验票机之间直线的时间，以及它将使用的铁路。 保证对于任何通过同一条铁路（即 $r_i = r_j$）的两列火车 $i$ 和 $j$，它们之间至少间隔 $1$ 秒（即要么 $a_j \ge b_i + 1$，要么 $a_i \ge b_j + 1$）。

输出 Isona 为了及时到达验票机而必须执行的最少速度变化次数。如果不可能，则打印 $-1$。

在第一个样例中，如果 Isona 在时间 $t=0$ 以最大速度（$1$ 米/秒）开始跑，她将在火车即将通过每条铁路时刚好穿过它，并在时间 $4 = s - 1$ 到达对面站台，且没有改变速度。 在第二个样例中，一个可能的包含 $2$ 次速度变化的方案如下：前 $2$ 秒 Isona 以最大速度（$0.5$ 米/秒）跑，然后她减速到 $0.25$ 米/秒跑 $4$ 秒直到到达第二条铁路。此时，她再次以最大速度跑直到到达对面站台。 在第三个样例中，Isona 可以在开始跑之前等待 $2$ 秒。然后她以最大速度（$0.5$ 米/秒）跑 $5$ 秒。之后，她静止（或以 $0$ 米/秒跑）等待 $1$ 秒，最后她再次以最大速度跑最后 $5$ 秒。总共，她改变了两次速度。 翻译由 DeepSeek 完成