P15189 [SWERC 2019] Icebergs

Tania 是一位海洋生物学家。她的目标是测量气候变化对马卡鲁尼企鹅种群的影响。与大多数企鹅物种一样，马卡鲁尼企鹅生活在南半球，靠近南极洲。Tania 主要关注“云岛”（Îles Nuageuses）附近的马卡鲁尼企鹅种群。 夏季，岛屿周围的冰层融化，岛屿变得太小，无法容纳所有鸟类。一些企鹅生活在漂浮的冰山上。为了她的研究，Tania 需要测量这些冰山的面积。 通过卫星图像和图像识别，Tania 获得了冰山的地图，而你的目标是测量它们的面积。Tania 研究的岛屿相当小，地球在局部可以近似为一个平面。因此，Tania 的地图使用通常的二维笛卡尔坐标系，面积按通常方式计算。例如，由不等式 $x_1 \leq x \leq x_2$ 和 $y_1 \leq y \leq y_2$ 定义的与坐标轴平行的矩形，其面积为 $(x_2 - x_1) \times (y_2 - y_1)$。 在 Tania 的表示中，冰山是一个由其边界表示的多边形。对于每个冰山，Tania 记录了定义冰山边界的点序列 $p_1, \ldots, p_k$。不同的冰山从不相互接触，也从不重叠。此外，冰山的边界 $p_1, \ldots, p_k$ 总是一个“简单”多边形，即线段 $[p_1; p_2], \ldots, [p_k; p_1]$ 中任意两条都不相交。

输入包含以下行： - 第一行，一个整数 $N$，描述多边形的数量； - 接下来是 $N$ 个文本块，每个描述一个多边形，每个块包含： - 第一行，一个整数 $P$，定义多边形边界的点的数量， - 接下来的 $P$ 行，每行两个空格分隔的整数 $x$ 和 $y$，每个边界点的坐标。

输出应包含一个整数：总面积向下取整到最接近的整数。换句话说，输出应为一行，包含一个整数 $I$，使得输入中描述的多边形的总面积 $A$ 满足 $I \leq A < I+1$。

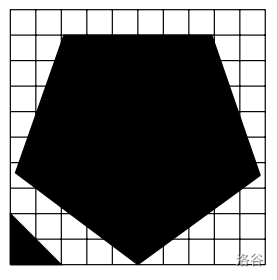
#### 样例解释 1 此样例中只有一个冰山，是一个边长为 1 的正方形。 #### 样例解释 2 在此样例中（如右图所示），有两个冰山，一个三角形面积为 $200$，一个五边形面积为 $5900.5$。 :::align{center}  ::: #### 数据范围 - 多边形数量 $N$ 满足 $1 \leq N \leq 1000$。 - 每个多边形由 $P$ 个点描述，$3 \leq P \leq 50$。 - 所有坐标满足 $0 \leq x, y \leq 10^6$。 翻译由 DeepSeek 完成