P15194 [SWERC 2019] Bird Watching

Kiara 正在研究一种行为方式非常奇特的鸟类。它们的移动最好用图的语言来解释：存在一个有向图 $G$，其节点是树木，只有当 $(T_a, T_b)$ 是 $G$ 的一条边时，鸟才能从一棵树 $T_a$ 飞到另一棵树 $T_b$。 Kiara 并不知道控制这些鸟类飞行的真实图 $G$，但在她之前的实地研究中，Kiara 收集了许多鸟类旅程的数据。利用这些数据，她构建了一个图 $P$ 来解释它们是如何移动的。Kiara 花了大量时间观察它们，因此她确信，如果一只鸟可以直接从 $a$ 飞到 $b$，那么她至少目击过一次这样的飞行。然而，有可能一只鸟的飞行路径是 $a$ 到 $b$ 再到 $c$，但她只目击了停靠点 $a$ 和 $c$，于是将 $(a, c)$ 添加到了 $P$ 中。也可能是一只鸟的飞行路径是 $a$ 到 $b$ 到 $c$ 再到 $d$，而她只目击了 $a$ 和 $d$，于是将 $(a, d)$ 添加到了 $P$ 中，等等。总而言之，她知道 $P$ 包含了 $G$ 的所有边，并且 $P$ 可能还包含一些其他的边 $(a, b)$，这些边在 $G$ 中存在一条从 $a$ 到 $b$ 的路径（注意，$P$ 可能并不包含所有这样的边）。 对于下一次实地研究，Kiara 决定将基地安置在一棵给定的树 $T$ 旁边。为了预警鸟类到达 $T$，她还希望在鸟类可能飞来的树木（即满足 $(T', T)$ 是 $G$ 中一条边的那些树 $T'$）上安装探测器。由于探测器价格不菲，她只希望在那些她确信 $(T', T)$ 属于 $G$ 的树 $T'$ 上安装探测器。 Kiara 确信一条边 $(a, b)$ 属于 $G$，当且仅当 $(a, b)$ 是 $P$ 的一条边，并且所有在 $P$ 中从 $a$ 开始、在 $b$ 结束的路径都使用了边 $(a, b)$。Kiara 请你计算集合 $S(T)$，即所有她确信 $(T', T)$ 是 $G$ 的一条边的树 $T'$。

输入描述图 $P$。第一行包含三个空格分隔的整数 $N$, $M$, 和 $T$：$N$ 是 $P$ 的节点数，$M$ 是 $P$ 的边数，$T$ 是 Kiara 将要安置基地的树所对应的节点。 接下来的 $M$ 行描述图 $P$ 的边。每行包含两个空格分隔的整数 $a$ 和 $b$（$0 \leq a, b < N$ 且 $a \neq b$），表示 $(a, b) \in P$。保证同一对 $(a, b)$ 不会出现两次。

你的输出应描述集合 $S(T)$。第一行应包含一个整数 $L$，即 $S(T)$ 中的节点数，接下来是 $L$ 行，每行包含 $S(T)$ 的一个不同元素。$S(T)$ 的元素应按升序打印，每行一个元素。

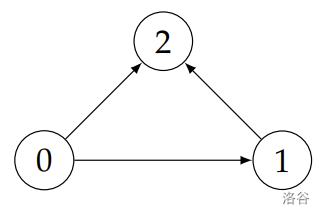
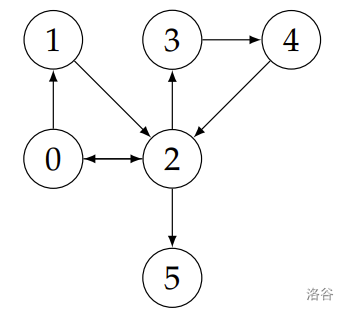
#### 样例解释 1 此示例对应的图如右图所示。节点 $1$ 属于 $S(2)$，因为（唯一）从 $1$ 到 $2$ 的路径使用了 $(1, 2)$。节点 $0$ 不属于 $S(2)$，因为路径 $0 \to 1 \to 2$ 没有使用边 $(0, 2)$。 :::align{center}  ::: #### 样例解释 2 此示例对应的图如右图所示。出于与样例 1 相同的原因，节点 $0$ 不属于 $S(2)$，而 $1$ 属于。节点 $3$ 和 $5$ 不属于 $S(2)$，因为我们没有边 $(3, 2)$ 或 $(5, 2)$。最后，$4$ 属于 $S(2)$，因为所有从 $4$ 到 $2$ 的路径都使用了边 $(4, 2)$。 :::align{center}  ::: #### 数据范围 - $1 \leq N, M \leq 100\,000$； - $0 \leq T < N$。 翻译由 DeepSeek 完成