P15203 [SWERC 2018] Travel Guide

Paris counts many hotels. Some are very close to the **Orly** airport, which is very useful to spend a night before an early flight. Some are very close to the **Notre-Dame** cathedral which allows tourists to walk around the “Île Saint-Louis” at dawn and enjoy the banks of the Seine. Finally, some are closer to the **Disneyland Paris** resort which is the most visited tourist attraction. Travelers who come to Paris usually want to stay near these three main Points Of Interest (POIs): **Orly**, **Notre-Dame**, and **Disneyland**. You are employed by a travel agency and your manager Anna wants to prepare a list of hotels to include in her new travel guide. Her guide contains one entry per station of the metropolitan network. Anna notices that some stations do not have a convenient location with respect to the distance to the three POIs and therefore her guide should not contain a hotel section for such “useless” stations. Anna considers that a station is *useless* when another station is closer to all the POIs. Formally a station $ A $ is useless when there exists another station $ B $ such that $ B $ is at least as close to the three POIs as $ A $ is and $ B $ is strictly closer than $ A $ to at least one of those POIs. A station is *useful* if it is not useless. Anna asks you how many stations in her guide will have a hotel section. To compute this list you are given the plan of the metropolitan network. The plan of the metropolitan network is an undirected weighted graph. In this graph, each node corresponds to a station (note that each POI is also a station); each edge links two stations and takes a certain time to be traversed in either direction. This graph is connected and the distance between any two stations is the lowest total time of a path between the two nodes.

The input comprises several lines, each consisting of integers separated with single spaces: - The first line consists of the number $ N $ of nodes and the number $ E $ of edges. - Each of the following $ E $ lines describes an edge with three integers $ A $, $ B $, and $ W $: - $ A $ and $ B $ are the endpoints of the edge (numbered from 0 to $ N - 1 $); - $ W $ is the weight of the edge. In the graph: - **Orly** corresponds to the station 0; - **Notre-Dame** corresponds to the station 1; - **Disneyland** corresponds to the station 2.

The output should consist of a single line, whose content is an integer, the number of useful stations.

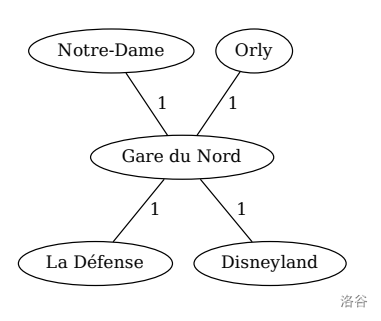
#### Sample Explanation 1 This graph is depicted on the right with **Gare du Nord** as node 3 and **La Défense** as node 4. In this graph, four stations are useful: **Orly**, **Disneyland**, **Notre-Dame** and **Gare du Nord**. The stations corresponding to **Orly**, **Disneyland**, **Notre-Dame** are the closest stations to themselves. All stations have a POI at distance 2 except for **Gare du Nord**, which is at distance 1 to all POIs. Finally, **La Défense** is useless because it is at distance 2 from all POIs. For instance, **Orly** is as close as **La Défense** to **Notre-Dame** and **Disneyland** but strictly closer to **Orly** and thus **Orly** witnesses that the station **La Défense** is useless. 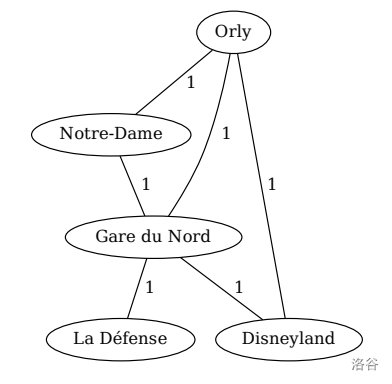:::align{center}  ::: #### Sample Explanation 2 In this graph (depicted on the right), three stations are useful: **Orly**, **Disneyland**, and **Notre-Dame**. The stations corresponding to **Orly**, **Disneyland**, **Notre-Dame** are the closest stations to themselves. All stations have a POI at distance 2 except for **Gare du Nord**, which is at distance 1 to all POIs, and **Orly** which is at distance 1 to all POIs but at distance of 0 to itself. Therefore **Gare du Nord** is useless. :::align{center}  ::: #### Limits - $ 4 \leq N \leq 100\,000 $; - $ E \leq 500\,000 $; - $ 1 \leq w \leq 100 $.