P15203 [SWERC 2018] Travel Guide

巴黎拥有众多酒店。其中一些酒店非常靠近 **奥利** 机场，这对于赶早班飞机的旅客来说非常方便。另一些则靠近 **巴黎圣母院** 教堂，方便游客在黎明时分漫步于“圣路易岛”，享受塞纳河畔的风光。还有一些则更靠近 **巴黎迪士尼乐园** 度假区，这是游客最多的旅游景点。前来巴黎的旅行者通常希望住在这三个主要兴趣点（POI）附近：**奥利**、**巴黎圣母院** 和 **迪士尼乐园**。 你受雇于一家旅行社，你的经理安娜想要准备一份酒店列表，收录到她新的旅行指南中。她的指南为地铁网络的每个站点都设有一个条目。安娜注意到，有些站点相对于这三个兴趣点的距离而言，地理位置并不便利，因此她的指南不应为这些“无用”站点包含酒店部分。 安娜认为，当一个站点在到达所有兴趣点的距离上都不如另一个站点近时，它就是 **无用的**。形式化地说，当存在另一个站点 $ B $，使得 $ B $ 到三个兴趣点的距离都至少与站点 $ A $ 一样近，并且 $ B $ 到其中至少一个兴趣点的距离严格比 $ A $ 更近时，站点 $ A $ 就是无用的。一个站点是 **有用的**，当且仅当它不是无用的。 安娜想请你计算她的指南中将有多少个站点会包含酒店部分。为了计算这个列表，你会得到地铁网络的平面图。地铁网络的平面图是一个无向加权图。在这个图中，每个节点对应一个站点（注意每个兴趣点本身也是一个站点）；每条边连接两个站点，并且可以在任意方向上以某个固定的时间通过。这个图是连通的，任意两个站点之间的距离是连接这两个节点的所有路径中总时间最短的那条路径的时间。

输入包含若干行，每行由用单个空格分隔的整数组成： - 第一行包含节点数 $ N $ 和边数 $ E $。 - 接下来的 $ E $ 行每行描述一条边，包含三个整数 $ A $、$ B $ 和 $ W $： - $ A $ 和 $ B $ 是边的两个端点（编号从 0 到 $ N - 1 $）； - $ W $ 是边的权重。 在图中： - **奥利** 对应站点 0； - **巴黎圣母院** 对应站点 1； - **迪士尼乐园** 对应站点 2。

输出应包含一行，内容为一个整数，即有用站点的数量。

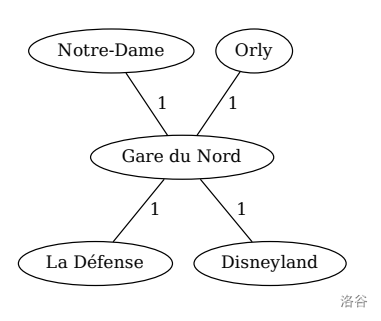
#### 样例解释 #1 该图如右侧所示，其中 **巴黎北站** 为节点 3，**拉德芳斯** 为节点 4。在此图中，有四个站点是有用的：**奥利**、**迪士尼乐园**、**巴黎圣母院** 和 **巴黎北站**。**奥利**、**迪士尼乐园**、**巴黎圣母院** 对应的站点是距离它们自身最近的站点。除了 **巴黎北站** 到所有兴趣点的距离为 1 之外，所有站点到某个兴趣点的距离都是 2。最后，**拉德芳斯** 是无用的，因为它到所有兴趣点的距离都是 2。例如，**奥利** 到 **巴黎圣母院** 和 **迪士尼乐园** 的距离与 **拉德芳斯** 相同，但到 **奥利** 本身的距离严格更近，因此 **奥利** 证明了站点 **拉德芳斯** 是无用的。 :::align{center}  ::: #### 样例解释 #2 在此图中（如右侧所示），有三个站点是有用的：**奥利**、**迪士尼乐园** 和 **巴黎圣母院**。**奥利**、**迪士尼乐园**、**巴黎圣母院** 对应的站点是距离它们自身最近的站点。除了 **巴黎北站** 到所有兴趣点的距离为 1，以及 **奥利** 到所有兴趣点的距离为 1（但到自身的距离为 0）之外，所有站点到某个兴趣点的距离都是 2。因此 **巴黎北站** 是无用的。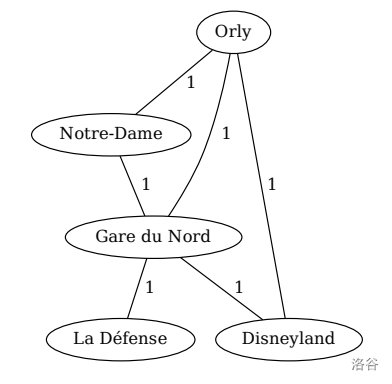 :::align{center}  ::: ### 数据范围 - $ 4 \leq N \leq 100\,000 $； - $ E \leq 500\,000 $； - $ 1 \leq w \leq 100 $。 翻译由 DeepSeek 完成