P15207 [NWERC 2025] Arcade Crane

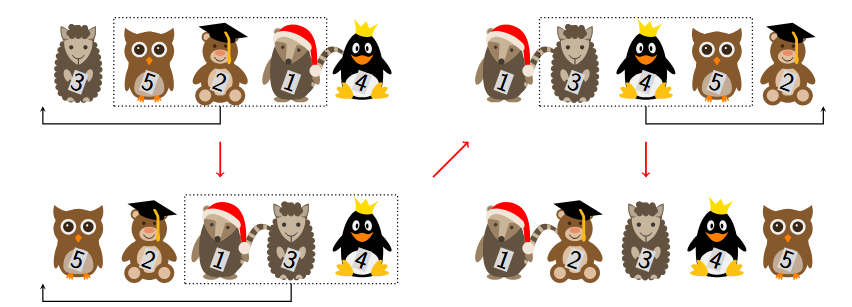
当地游戏厅刚刚安装了一款新游戏，这是对经典抓娃娃机的一种新尝试。 机器内部有 $n$ 个毛绒玩具排成一排，在这排玩具上方有一个由硬币操作的机械爪。 每投入一枚硬币，爪子可以使用一次，从一排中抓取恰好三个连续的毛绒玩具，然后将它们重新插入到这排中的某个位置。 剩余的毛绒玩具总是可以被推来推去（不改变它们的顺序）以为重新插入腾出空间。 游戏的目标是按可爱度对毛绒玩具进行排序，一旦它们被排序，机器就会打开，实现这一目标的人将赢得**所有**毛绒玩具。  **图 A.1：样例输出 1 的图示。** Uli 非常想赢得这些毛绒玩具，因此他们做了一些研究，发现每个毛绒玩具都有一个从 $1$ 到 $n$ 的独特可爱度值。 为了获胜，他们需要将这些毛绒玩具按这些值的递增顺序排序。 在知道了所有可爱度值并拥有大量 $5000$ 枚硬币的情况下，他们应该如何操作机器以确保赢得毛绒玩具？

输入包括： * 一行，一个整数 $n$ ($5 \le n \le 1000$)，表示毛绒玩具的数量。 * 一行，$n$ 个不同的整数 $a_1, ..., a_n$（对于每个 $i$，$1 \le a_i \le n$），其中 $a_i$ 是第 $i$ 个毛绒玩具的可爱度值。

首先，输出一个整数 $q$ ($0 \le q \le 5000$)，表示操作的数量。 然后输出 $q$ 对整数 $i$ 和 $j$ ($1 \le i, j \le n-2$)，按顺序描述操作。 机器中毛绒玩具的位置从 $1$ 到 $n$ 编号。 在一个由 $i$ 和 $j$ 描述的操作中，位置 $i, i+1$ 和 $i+2$ 的毛绒玩具被抓取，然后重新插入到序列中，使得它们在操作后处于位置 $j, j+1$ 和 $j+2$。 可以证明，使用最多 $5000$ 次操作的解总是存在的。 如果有多个有效解，你可以输出其中任意一个。特别是，你不需要最小化操作次数。

对于样例 #4：**注意**，允许 $i = j$（这不会改变序列）。 对于这个测试用例，也允许不使用任何操作，只输出 "0"。