P15207 Arcade Crane

The local arcade just installed a new game, which is a new take on the classic claw machine. Inside the machine, there are $n$ plushies arranged in a row, and above this row there is a mechanical claw which is operated by coins. For each coin inserted into the machine, the claw can be used once to grab exactly three consecutive plushies out of the row and then re-insert them somewhere in the row. The remaining plushies can always be pushed around (without changing their order) to make room for the re-insertion. The goal of the game is to sort the plushies by cuteness, and once they are sorted, the machine opens up and the person who achieves this wins **all** the plushies.  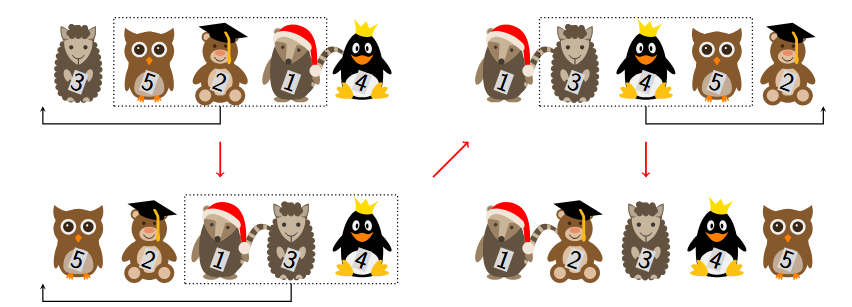**Figure A.1: Illustration of Sample Output 1.** Uli really wants to win the plushies, so they have done some research and found out that each plushie has a distinct cuteness value from $1$ to $n$. To win, they need to sort the plushies in increasing order of these values. Equipped with the knowledge of all the cuteness values and a large stash of $5000$ coins, how can they operate the machine to ensure they win the plushies?

The input consists of: * One line with an integer $n$ ($5 \le n \le 1000$), the number of plushies. * One line with $n$ distinct integers $a_1, ..., a_n$ (for each $i$, $1 \le a_i \le n$), where $a_i$ is the cuteness value of the $i$th plushie.

First, output an integer $q$ ($0 \le q \le 5000$), the number of operations. Then output $q$ pairs of integers $i$ and $j$ ($1 \le i, j \le n-2$), describing the operations in order. The plushie positions in the machine are indexed from $1$ to $n$. In an operation described by $i$ and $j$, the plushies at positions $i, i+1$ and $i+2$ are grabbed and then re-inserted into the sequence such that they are in positions $j, j+1$ and $j+2$ after the operation. It can be shown that a solution using at most $5000$ operations always exists. If there are multiple valid solutions, you may output any one of them. In particular, you do not need to minimize the number of operations.

Explanation on Sample #4. **Note** that $i = j$ is allowed (this does not change the sequence). For this test case, it would also be allowed to use no operations at all and just output "0".