P15209 Canal Crossing

To escape from the Christmas market hassle, you are planning a trip to Venice to see its beautiful canals and its many bridges. Unfortunately, you do not seem to be the only person with that plan, and Venice recently decided to charge for that pleasure. Therefore, you decide that crossing each bridge once is enough for you. Fortunately, every place can be reached from any other place using only streets, without crossing any bridges. Interestingly, there is exactly one way to reach any other place using only streets. After you gathered all this knowledge, now all that is left is to plan a trip that crosses each bridge exactly once. To keep things interesting, you also want to use each street at most once. What is the length of the shortest possible trip? Note that your tour can start at any place you choose, but it has to end where it starts.  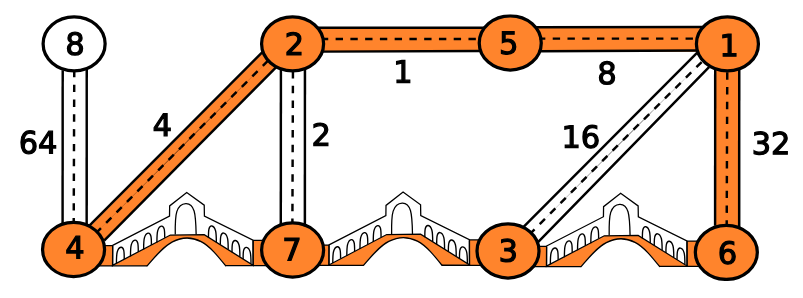Figure **C.1**: Illustration of Sample Input **1** with a tour of length $45$.

The input consists of: * One line with an integer $n$ ($3 \le n \le 10^5$), the number of places in Venice. * $n-1$ lines, each with three integers $a, b,$ and $w$ ($1 \le a, b \le n, a \ne b, 1 \le w \le 10^6$), the starting and ending place of each street and its length. * One line with an integer $m$ ($1 \le m \le 5 \cdot 10^5$), the number of bridges in Venice. * $m$ lines, each with two integers $a$ and $b$ ($1 \le a, b \le n, a \ne b$), the places where each bridge starts and ends. Bridges are short, and thus have length zero. It is guaranteed that every place can be reached from any other place without using any bridges. Further, no bridge connects two places which are directly connected by a street, and all bridges are between distinct pairs of places. Lastly, it is guaranteed that at least one tour exists that crosses each bridge exactly once and uses every street at most once.

Output the length of the shortest tour that crosses all bridges and uses each street at most once.