P15214 Illuminated Stalls

Year after year, you have strolled through the Christmas market, catching up with old friends over mulled wine. Lately the prices have been absurd, and just a few evenings leave you in the financial ruin. This year, you decided to turn things around and open a stall selling mulled wine. But competition is fierce, and it turns out that yet another absurdly overpriced stall is far less profitable than you hoped. To stand out, you created a difficult puzzle. If a customer solves it, they can drink as much mulled wine as they want for free. Naive customers are often willing to pay more than usual. This puzzle consists of $n$ line-shaped neon light tubes hanging on the wall. They are oriented either horizontally or vertically. No two horizontal lights overlap or touch and no two vertical lights overlap or touch, but a vertical light can intersect or touch a horizontal light. The player is allowed to rotate and/or move at most one light tube in any way they like. The goal is to have at least one illuminated neon light square. All four sides of this square have to be fully covered by neon lights, but the lights can be longer than the sides of the square. Lights are allowed to lie in the interior of the square or intersect its sides. The light that is moved is allowed to be placed such that it touches, partially overlaps, or fully overlaps other collinear lights. You want to make this puzzle as hard as possible, but if there is no valid solution, you will get into trouble with the German lawmakers, as regulations are very strict. Given a puzzle, find out whether there is a way to make a square by moving and/or rotating at most one light.

The input consists of: * One line with an integer $t$ ($1 \le t \le 20000$), the number of test cases. * For each test case, the input consists of: * One line with an integer $n$ ($4 \le n \le 2 \cdot 10^5$), the number of neon light tubes. * $n$ lines, each with four integers $x_1, y_1, x_2$, and $y_2$ ($0 \le x_1, y_1, x_2, y_2 \le 10^9, x_1 \le x_2, y_1 \le y_2$, and either $x_1 = x_2$ or $y_1 = y_2$, but not both), where $(x_1, y_1)$ and $(x_2, y_2)$ are the endpoints of a light tube. The total number of light tubes over all test cases is at most $2 \cdot 10^5$. All light tubes are either vertical or horizontal. For every test case, the initial configuration has no two overlapping or touching horizontal lights, and also has no two overlapping or touching vertical lights. Note that horizontal lights can intersect and touch vertical lights.

For each test case, output "yes" if there is a way to make a square by moving and/or rotating at most one light, otherwise output "no".

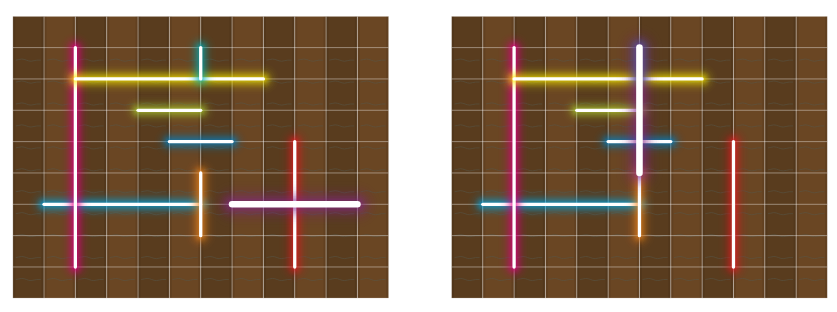
 Figure $\text{I.1}$: On the left, the initial configuration of lights of the fifth test case of Sample Input $1$ is shown. On the right, the purple neon light was rotated and moved to make a $4 \times 4$ square.