P15214 [NWERC 2025] Illuminated Stalls

年复一年，你漫步在圣诞市场，一边喝着热红酒一边与老朋友叙旧。 最近价格已经变得荒谬，仅仅几个晚上就让你陷入财务困境。 今年，你决定扭转局面，开一个卖热红酒的摊位。 但竞争很激烈，结果又一个价格高得离谱的摊位远不如你希望的那么有利可图。 为了脱颖而出，你设计了一个难题。 如果顾客解开了它，他们就可以免费喝到他们想要的任意多的热红酒。 天真的顾客通常愿意支付比平常更多的钱。 这个谜题由挂在墙上的 $n$ 个直线形状的霓虹灯管组成。 它们的朝向要么是水平的，要么是垂直的。 没有两个水平灯管重叠或接触，也没有两个垂直灯管重叠或接触，但垂直灯管可以与水平灯管相交或接触。 玩家最多可以按照他们喜欢的任何方式旋转和/或移动一个灯管。 目标是至少有一个发光的霓虹灯正方形。 这个正方形的四条边必须完全被霓虹灯覆盖，但灯的长度可以比正方形的边长长。 灯管允许位于正方形的内部或与其边相交。 被移动的灯管可以放置成与其他共线的灯管接触、部分重叠或完全重叠。 你想让这个谜题尽可能难，但如果没有有效的解决方案，你将遇到德国立法者的麻烦，因为法规非常严格。 给定一个谜题，找出是否有一种方法，通过移动和/或旋转最多一个灯管来构成一个正方形。

输入包括： * 一行一个整数 $t$ ($1 \le t \le 20000$)，表示测试用例的数量。 * 对于每个测试用例，输入包括： * 一行一个整数 $n$ ($4 \le n \le 2 \cdot 10^5$)，表示霓虹灯管的数量。 * $n$ 行，每行四个整数 $x_1, y_1, x_2$ 和 $y_2$ ($0 \le x_1, y_1, x_2, y_2 \le 10^9, x_1 \le x_2, y_1 \le y_2$，且要么 $x_1 = x_2$，要么 $y_1 = y_2$，但不同时满足)，其中 $(x_1, y_1)$ 和 $(x_2, y_2)$ 是一个灯管的端点。 所有测试用例的灯管总数不超过 $2 \cdot 10^5$。 所有灯管要么是垂直的，要么是水平的。 对于每个测试用例，初始配置中没有两个水平灯管重叠或接触，也没有两个垂直灯管重叠或接触。 注意水平灯管可以与垂直灯管相交或接触。

对于每个测试用例，如果有一种方法通过移动和/或旋转最多一个灯管来构成一个正方形，则输出 "yes"，否则输出 "no"。

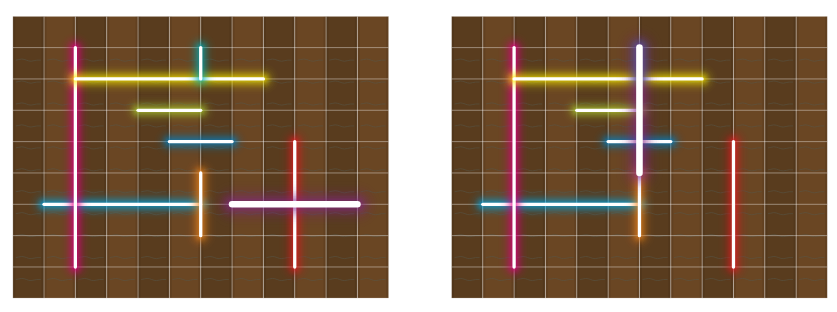
 图 $\text{I.1}$：左边显示了样例输入 $1$ 的第五个测试用例的初始灯管配置。右边，紫色的霓虹灯被旋转和移动以构成一个 $4 \times 4$ 的正方形。