P15224 [SWERC 2017] Cordon Bleu

一位巴黎企业家刚开了一家新餐厅 “Au bon cordon bleu”，以一道著名的法国菜命名。然而，没有人知道哪种葡萄酒适合搭配这道菜。这位企业家计划品尝多种不同的葡萄酒，以构建酒单。 他计划品尝的各种葡萄酒瓶可以从位于巴黎或其周边的不同酒商处获得。作为一种非常敏感的产品，高品质葡萄酒只能由训练有素的摩托车快递员运送。因此，这些快递员非常昂贵。 一个快递员可以用于运送多个葡萄酒瓶，但一次只能运送一个瓶子。所有快递员的报酬按相同固定费率支付：每公里一欧元。使用的距离函数是行程中每个单独片段的曼哈顿距离（也称为出租车几何距离）：从点 $(x_1, y_1)$ 到点 $(x_2, y_2)$ 的距离为 $|x_1 - x_2| + |y_1 - y_2|$。 负责运送单个葡萄酒瓶的快递员将获得报酬，金额等于以下两个（曼哈顿）距离之和：从她的基地到酒商地点，以及从酒商地点到餐厅。 考虑一个更复杂的例子：一个快递员负责依次运送两个葡萄酒瓶。支付的金额将是以下距离之和：从他的基地到第一个瓶子的位置，然后到餐厅，接着到第二个瓶子的位置，然后到餐厅。 帮助这位企业家最小化雇佣快递员的成本。给定一组对应可用快递员的笛卡尔坐标、一组对应需要收集的珍贵葡萄酒瓶位置的笛卡尔坐标以及餐厅的位置，计算快递员将被支付的最小公里数。没有义务使用所有可用快递员，瓶子可以按任意顺序收集。

输入包含若干行，每行由空格分隔的整数组成： - 第一行包含需要收集的葡萄酒瓶数量 $N$ 和可用快递员数量 $M$。 - 接下来的 $N$ 行每行包含每个瓶子的坐标，即两个整数 $x$ 和 $y$。 - 接下来的 $M$ 行每行包含每个快递员基地的坐标，即两个整数 $x$ 和 $y$。 - 最后一行包含餐厅的坐标，即两个整数 $x$ 和 $y$。

一个整数：需要支付以收集所有瓶子的最小欧元数。

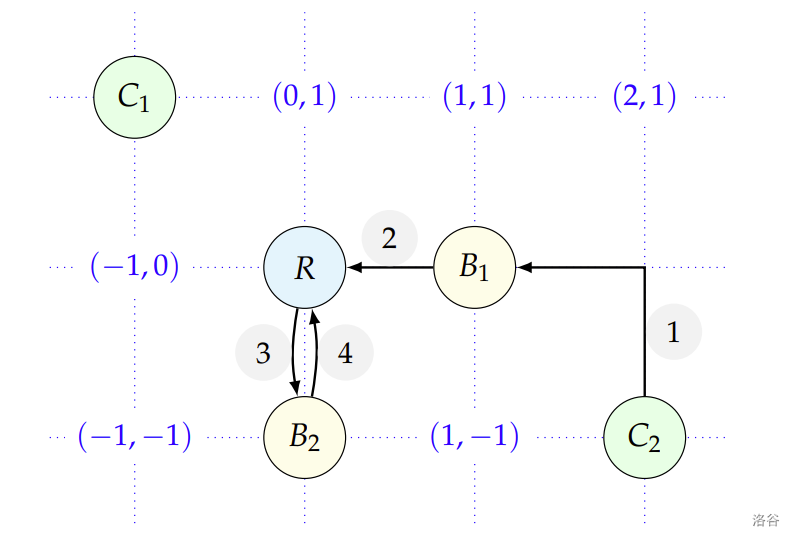
#### 注意 可能有多个物品位于相同的初始位置。例如，两个瓶子、十个快递员和餐厅可能共享同一个起始位置。 #### 样例解释 :::align{center}  ::: 在这个例子中，只有一个快递员（$C_2$）被用来取回两个瓶子 $B_1$ 和 $B_2$，并通过依次执行标记为 1 到 4 的移动将它们带到餐厅 $R$。总公里数为 5。这是最优解之一。 ### 数据范围 - $1 \leq N \leq 1000$； - $1 \leq M \leq 1000$； - 所有坐标 $(x, y)$ 满足 $-1000 \leq x \leq 1000$ 且 $-1000 \leq y \leq 1000$。 翻译由 DeepSeek 完成