P15227 [SWERC 2017] Frosting on the Cake
题目描述
面包师 Iskander 正在装饰一个巨大的蛋糕,将蛋糕的矩形表面覆盖上糖霜。为此,他将糖霜糖与柠檬汁和食用色素混合,以产生三种糖霜:黄色、粉色和白色。这些颜色用数字标识:0 代表黄色,1 代表粉色,2 代表白色。
为了获得漂亮的图案,他将蛋糕表面划分为宽度分别为 $A_1, A_2, \ldots, A_n$ 厘米的垂直条纹和高度分别为 $B_1, B_2, \ldots, B_n$ 厘米的水平条纹,其中 $n$ 是一个正整数。这些条纹将蛋糕表面分割成 $n \times n$ 个矩形。对于所有 $1 \leq i, j \leq n$ ,垂直条纹 $i$ 和水平条纹 $j$ 的交集处的颜色编号为 $(i + j) \bmod 3$ 。为了准备糖霜,Iskander 想知道三种颜色各自需要着色的总面积(平方厘米),并请求你的帮助。
:::aligned{center}
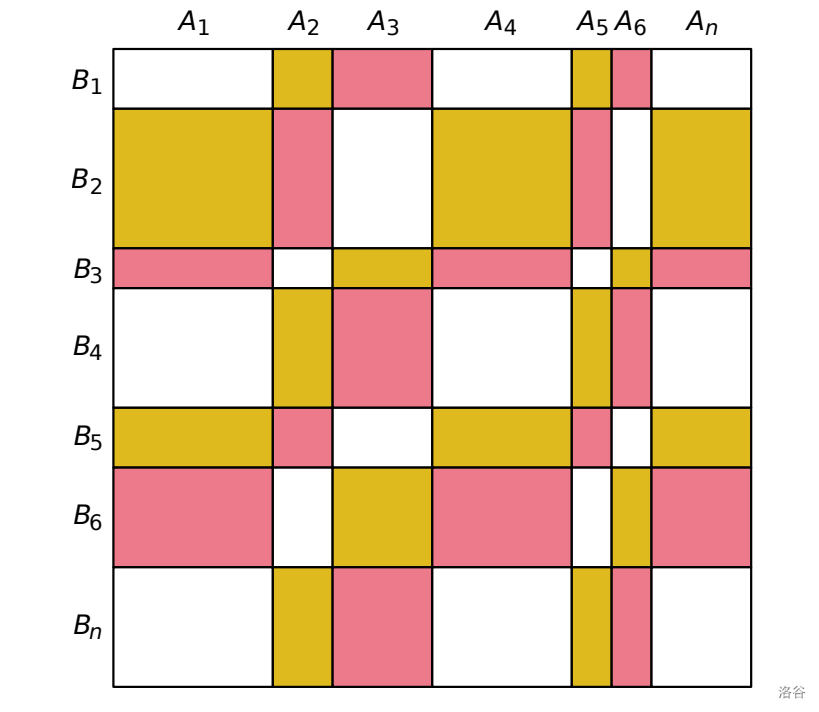
:::
输入格式
输入包含以下整数:
- 第一行:整数 $n$ ;
- 第二行: $A_1, \ldots, A_n$ 的值, $n$ 个整数,用单个空格分隔;
- 第三行: $B_1, \ldots, B_n$ 的值, $n$ 个整数,用单个空格分隔。
输出格式
输出应包含三个用单个空格分隔的整数,分别代表颜色 0 、1 和 2 的总面积。
说明/提示
#### 样例解释
对于样例 #1,蛋糕被均匀分割为 $3 \times 3$ 个边长为 1 厘米的正方形,每个颜色各占 3 个正方形,因此面积均为 3 平方厘米。
对于样例 #2,根据给定的条纹宽度和高度计算每种颜色的总面积,得到如输出所示的结果。
### 数据范围
输入满足 $3 \leq n \leq 100\,000$ 且 $1 \leq A_1, \ldots, A_n, B_1, \ldots, B_n \leq 10\,000$ 。
翻译由 DeepSeek 完成