P15239 [NHSPC 2025] Chomp!

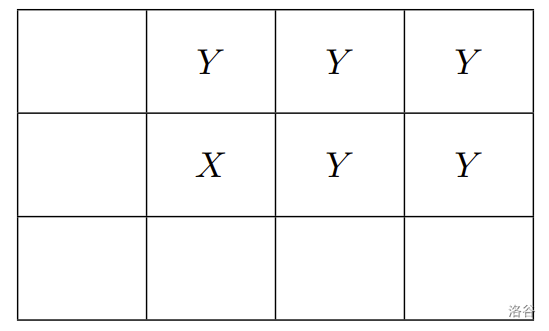
$\textit{Chomp!}$ 是一個經典的兩人遊戲。起始時有一片由 $mn$ 塊大小為 $1 \times 1$ 的小塊巧克力連為一片的巧克力，形狀如 $m \times n$ 的二維陣列（其中 $m$ 為列，$n$ 為行），而最左下角的那一小塊非常苦澀，大家都想避開。遊戲的玩法為輪流拿走巧克力小塊，方式是先從剩下來的巧克力挑一小塊，並把其右上方（含正上方及正右方）所有小塊同時拿掉。到最後誰拿到最左下角的那一小塊便輸了。 例如起始時有 $3 \times 4$ 的一片巧克力： :::align{center}  ::: 若玩家一選擇了 $X$ 那一小塊，則連帶 $Y$ 的那些小塊也會被拿掉： :::align{center}  ::: 接著由玩家二從剩下的巧克力塊選擇。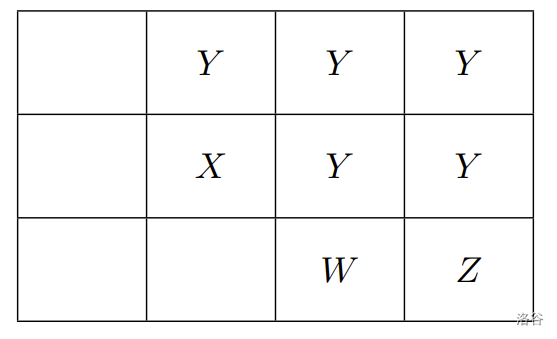若玩家二此時選擇了 $W$ 那一小塊，則連帶 $Z$ 的那些小塊也會被拿掉： :::align{center}  ::: 按照以上規則，我們不難證明，在遊戲中所出現的任何情形，如從左至右輸出每一行 (column) 的巧克力小塊數，其結果必為一單調遞減 (monotonic decreasing) 數列，且對應此數列之形狀唯一。如上述範例的最終狀態，其可以數列 $(3, 1, 0, 0)$ 表示。 在此題目中，我們針對 $3 \times n$ 大小巧克力的 $\textit{Chomp!}$ 遊戲中出現的各種情況進行分析，目的是計算在當前的情況下，先行者是否有獲勝的走法。我們假設遊戲雙方皆絕頂聰明，會採取最好的遊玩策略來讓自己獲勝。若先行者能獲勝，我們輸出在目前情況下有多少種可以獲勝的第一步選擇，並把這些選擇枚舉出來；反之，則輸出 $0$。這裡，我們將下面數上來第 $i$ 列、左邊數過來第 $j$ 行的小塊巧克力編號為 $(i, j)$，滿足左下角為 $(1, 1)$，右上角為 $(3, n)$。

$$ \begin{aligned} &t \\ &n_1 \; p_1 \; q_1 \; r_1 \\ &\vdots \\ &n_t \; p_t \; q_t \; r_t \end{aligned} $$ * $t$ 代表總共有 $t$ 筆詢問。 * $n_i$ 代表第 $i$ 筆詢問的巧克力總行數。 * $p_i, q_i, r_i$ 代表第 $i$ 筆詢問的狀態為從左至右先有 $p_i$ 行為 $3$ 小塊巧克力，接著有 $q_i$ 行為 $2$ 小塊巧克力，再有 $r_i$ 行為 $1$ 小塊巧克力。

$$ \begin{aligned} &c_1 \\ &x_{1,1} \; y_{1,1} \; \dots \; x_{1,c_{1}} \; y_{1,c_{1}} \\ &\vdots \\ &c_t \\ &x_{t,1} \; y_{t,1} \; \dots \; x_{t,c_{t}} \; y_{t,c_{t}} \end{aligned} $$ * $c_i$ 代表在第 $i$ 筆詢問的狀態下，先行者可以獲勝的第一步選擇數。若先行者無法獲勝，則 $c_i = 0$。 * $x_{i,j}, y_{i,j}$ 代表第 $i$ 筆詢問中，第 $j$ 個可以作為先行者獲勝的第一步選擇的小塊巧克力編號。若 $c_i > 1$，請依 $x$ 值小到大排序編號，若 $x$ 值相同則依 $y$ 值小到大排序編號。

### 測資限制 * $1 \le t \le 1000$。 * $1 \le n_i \le 500$。 * $0 \le p_i, q_i, r_i \le n_i$。 * $1 \le p_i + q_i + r_i \le n_i$。 * 輸入的數皆為整數。 ### 評分說明 本題共有三組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | 20 | $t = 1$，$p_i = 0$。 | | 2 | 37 | $1 \le n_i \le 50$。 | | 3 | 43 | 無額外限制。 |