P15243 [NHSPC 2025] 融合图的直径

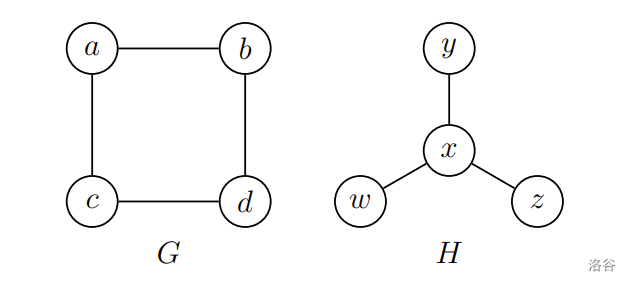
图形结构 $G=(V, E)$ 包含一个有限的集合 $V(G)$ 作为节点集合，以及一个无序对的集合 $E(G)$ 作为边的集合（如图一）。图形结构有相当广泛的应用，例如：交通路网、蛋白质结构的分析、计划管理评估、都市系统结构分析、半导体芯片设计元件摆放的布线等，使得图形结构一直是数学家和计算机科学家解决问题的好工具。 :::align{center}  图一 ::: 在数学中，两个集合 $A$ 和 $B$ 的笛卡儿积 (Cartesian product)，在集合论中表示为 $A \times B$，是所有可能的有序对组成的集合，其中有序对的第一个对象是 $A$ 的成员，第二个对象是 $B$ 的成员。图形理论学家 $Ray$ 教授研究图形性质多年，他定义两图形 $G$ 与 $H$ 的融合图为一个新的图形结构并以 $G \times H$ 表示，其点集合为 $V(G) \times V(H)$，此图形中若两节点 $(u, v)$ 与 $(u^\prime, v^\prime)$ 相连必须满足： - $u = u^\prime$ 且 $\{v, v^\prime\} \in E(H)$，或 - $v = v^\prime$ 且 $\{u, u^\prime\} \in E(G)$。 图二显示了图一中 $G$ 和 $H$ 的笛卡儿积。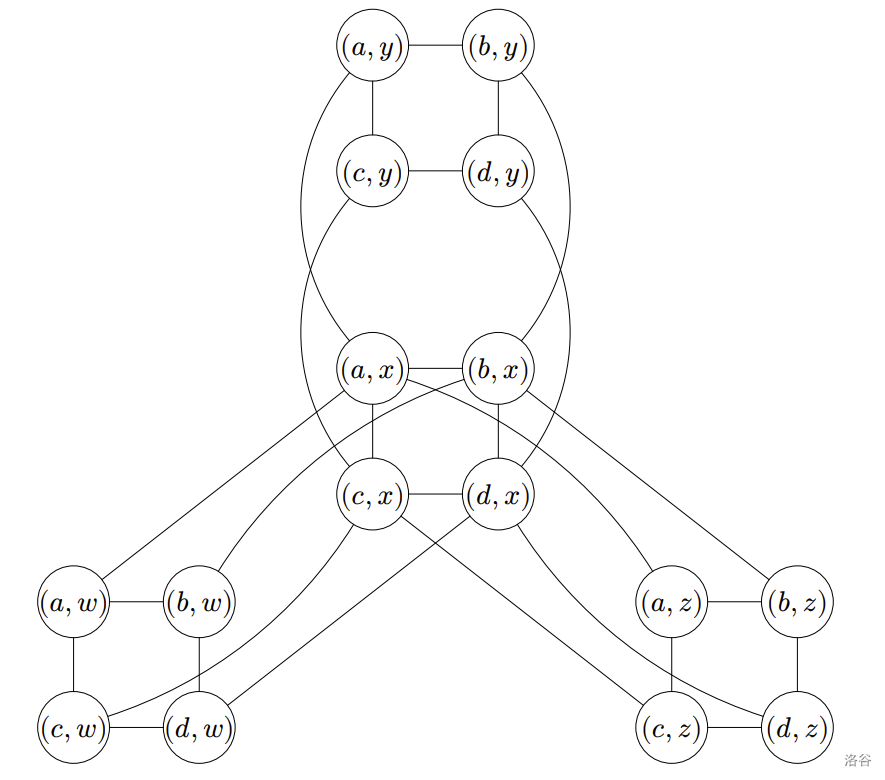 :::align{center}  图二 ::: $Ray$ 教授为了要进一步了解融合图的性质，他定义了一些度量方式：图形中任两节点 $x$ 和 $y$ 的距离是指从 $x$ 到 $y$ 之间，所经过边个数最小的路径其边的个数。若要计算一张图的直径，首先要求得任意两点之间的最短路径，在所有这些最短路径中，取其长度最长者，即是这张图的直径（如图三）。给定两张图形 $G$ 与 $H$，请协助 $Ray$ 教授计算融合图 $G \times H$ 的直径。假如答案大于或等于 $10^9+7$，则输出除以 $10^9+7$ 之后的余数；若没有答案，意即存在两点之间没有路径，则输出 $-1$。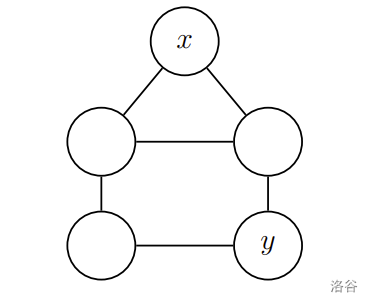 :::align{center}  图三：此图直径为 $2$ :::

$$ \begin{aligned} &n_1 \\ &e_{1,1} e_{1,2} \dots e_{1,n_1} \\ &e_{2,1} e_{2,2} \dots e_{2,n_1} \\ &\vdots \\ &e_{n_1,1} e_{n_1,2} \dots e_{n_1,n_1} \\ &n_2 \\ &e^\prime_{1,1} e^\prime_{1,2} \dots e^\prime_{1,n_2} \\ &e^\prime_{2,1} e^\prime_{2,2} \dots e^\prime_{2,n_2} \\ &\vdots \\ &e^\prime_{n_2,1} e^\prime_{n_2,2} \dots e^\prime_{n_2,n_2} \end{aligned} $$ - $n_1$ 代表图 $G$ 中的节点个数，即 $\left\vert V( G )\right\vert$。 - $e_{i,j}$ 代表图 $G$ 中，$i$ 和 $j$ 是否相连，其中 $e_{i,j}=1$ 代表有相连，$e_{i,j}=0$ 则代表没有相连。 - $n_2$ 代表图 $H$ 中的节点个数，即 $\left\vert V( H )\right\vert$。 - $e^\prime_{i,j}$ 代表图 $H$ 中，$i$ 和 $j$ 是否相连，其中 $e^\prime_{i,j}=1$ 代表有相连，$e^\prime_{i,j}=0$ 则代表没有相连。

$$D$$ - 如果直径存在，则 $D$ 代表融合图 $G\times H$ 的直径除以 $10^9+7$ 之后的余数。 - 如果直径不存在，则 $D = -1$。

### 数据限制 * $1 \leq n_1 \leq 2000$。 * $e_{i,j} \in \lbrace 0, 1 \rbrace$。 * $\forall 1 \leq i < j \leq n_1, e_{i,j}=e_{j,i}$。 * 保证图 $G$ 没有自环，也就是 $\forall 1\le i\le n_1, e_{i,i}=0$。 * $1 \leq n_2 \leq 2000$。 * $e^\prime_{i,j} \in \lbrace 0, 1 \rbrace$。 * $\forall 1 \leq i < j \leq n_2, e^\prime_{i,j}=e^\prime_{j,i}$。 * 保证图 $H$ 没有自环，也就是 $\forall 1\le i\le n_2, e^\prime_{i,i}=0$。 ### 评分说明 本题共有四组子任务，条件限制如下所示。 定义 $m_1,m_2$ 依序为图 $G$、图 $H$ 边的个数，也就是 $m_1=\left\vert E(G)\right\vert, m_2=\left\vert E(H)\right\vert$。 每一组可有一或多笔测试资料，该组所有测试资料皆需答对才会获得该组分数。 | 子任务 | 分数 | 额外输入限制 | | :------: | :----: | ------------ | | 1 | 18 | $n_1, m_1 \leq 400$，$n_2=1$ 且 $m_2=0$。 | | 2 | 11 | 保证 $G$ 和 $H$ 都是没有环的连通图。 | | 3 | 25 | $m_1, m_2 \leq 4000$。 | | 4 | 46 | 无额外限制。|