P15243 [NHSPC 2025] 融合圖的直徑

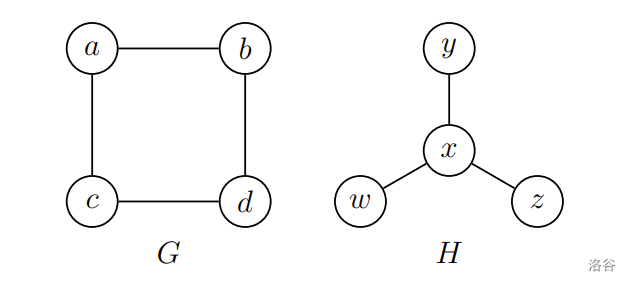
圖形結構 $G=(V, G)$ 包含一個有限的集合 $V(G)$ 做為節點集合，以及一個無序對的集合 $E(G)$ 作為邊的集合（如圖一）。圖形結構有相當廣泛的應用，例如：交通路網、蛋白質結構的分析、計畫管理評估、都市系統結構分析、半導體晶片設計元件擺放的布線等，使得圖形結構一直是數學家和電腦科學家解決問題的好工具。 :::align{center}  圖一 ::: 在數學中，兩個集合 $A$ 和 $B$ 的笛卡兒乘積 (Cartesian product)，在集合論中表示為 $A \times B$，是所有可能的有序對組成的集合，其中有序對的第一個對象是 $A$ 的成員，第二個對象是 $B$ 的成員。圖形理論學家 $Ray$ 教授研究圖形性質多年，他定義兩圖形 $G$ 與 $H$ 的融合圖為一個新的圖形結構並以 $G \times H$ 表示，其點集合為 $V(G) \times V(H)$，此圖形中若兩節點 $(u, v)$ 與 $(u^\prime, v^\prime)$ 相連必須滿足： - $u = u^\prime$ 且 $\{v, v^\prime\} \in E(H)$，或 - $v = v^\prime$ 且 $\{u, u^\prime\} \in E(G)$。 圖二顯示了圖一中 $G$ 和 $H$ 的笛卡兒乘積。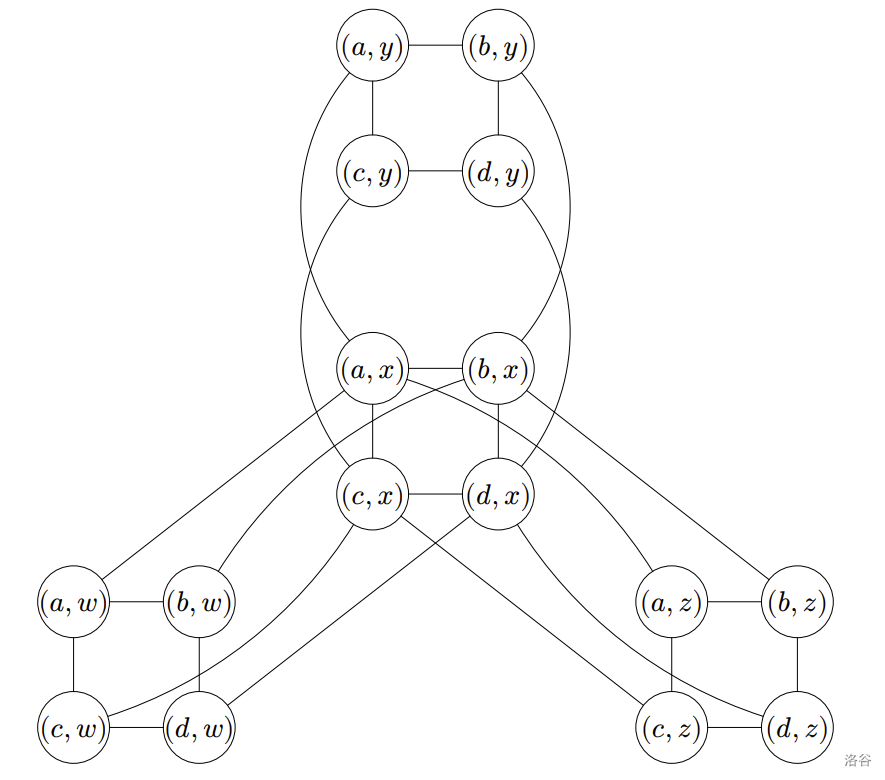 :::align{center}  圖二 ::: $Ray$ 教授為了要進一步瞭解融合圖的性質，他定義了一些度量方式：圖形中任兩節點 $x$ 和 $y$ 的距離是指從 $x$ 到 $y$ 之間，所經過邊個數最小的路徑其邊的個數。若要計算一張圖的直徑，首先要求得任意兩點之間的最短路徑，在這些所有的最短路徑中，取其長度最長者，即是這張圖的直徑（如圖三）。給定兩張圖形 $G$ 與 $H$，請協助 $Ray$ 教授計算融合圖 $G \times H$ 的直徑。假如答案大於或等於 $10^9+7$，則輸出除以 $10^9+7$ 之後的餘數；若沒有答案，意即存在兩點之間沒有路徑，則輸出 $-1$。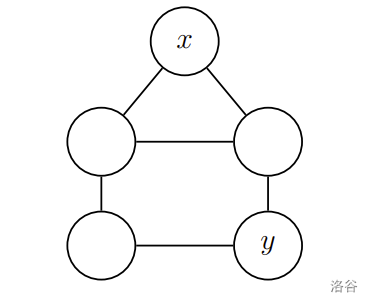 :::align{center}  圖三：此圖直徑為 $2$ :::

$$ \begin{aligned} &n_1 \\ &e_{1,1} e_{1,2} \dots e_{1,n_1} \\ &e_{2,1} e_{2,2} \dots e_{2,n_1} \\ &\vdots \\ &e_{n_1,1} e_{n_1,2} \dots e_{n_1,n_1} \\ &n_2 \\ &e^\prime_{1,1} e^\prime_{1,2} \dots e^\prime_{1,n_2} \\ &e^\prime_{2,1} e^\prime_{2,2} \dots e^\prime_{2,n_2} \\ &\vdots \\ &e^\prime_{n_2,1} e^\prime_{n_2,2} \dots e^\prime_{n_2,n_2} \end{aligned} $$ - $n_1$ 代表圖 $G$ 中的節點個數，即 $\left\vert V( G )\right\vert$。 - $e_{i,j}$ 代表圖 $G$ 中，$i$ 和 $j$ 是否相連，其中 $e_{i,j}=1$ 代表有相連，$e_{i,j}=0$ 則代表沒有相連。 - $n_2$ 代表圖 $H$ 中的節點個數，即 $\left\vert V( H )\right\vert$。 - $e^\prime_{i,j}$ 代表圖 $H$ 中，$i$ 和 $j$ 是否相連，其中 $e^\prime_{i,j}=1$ 代表有相連，$e^\prime_{i,j}=0$ 則代表沒有相連。

$$D$$ - 如果直徑存在，則 $D$ 代表融合圖 $G\times H$ 的直徑除以 $10^9+7$ 之後的餘數。 - 如果直徑不存在，則 $D = -1$。

### 測資限制 * $1 \leq n_1 \leq 2000$。 * $e_{i,j} \in \lbrace 0, 1 \rbrace$。 * $\forall 1 \leq i < j \leq n_1, e_{i,j}=e_{j,i}$。 * 保證圖 $G$ 沒有自環，也就是 $\forall 1\le i\le n_1, e_{i,i}=0$。 * $1 \leq n_2 \leq 2000$。 * $e^\prime_{i,j} \in \lbrace 0, 1 \rbrace$。 * $\forall 1 \leq i < j \leq n_2, e^\prime_{i,j}=e^\prime_{j,i}$。 * 保證圖 $H$ 沒有自環，也就是 $\forall 1\le i\le n_2, e^\prime_{i,i}=0$。 ### 評分說明 本題共有四組子任務，條件限制如下所示。 定義 $m_1,m_2$ 依序為圖 $G$、圖 $H$ 邊的個數，也就是 $m_1=\left\vert E(G)\right\vert, m_2=\left\vert E(H)\right\vert$。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | 18 | $n_1, m_1 \leq 400$，$n_2=1$ 且 $m_2=0$。 | | 2 | 11 | 保證 $G$ 和 $H$ 都是沒有環的連通圖。 | | 3 | 25 | $m_1, m_2 \leq 4000$。 | | 4 | 46 | 無額外限制。|