P15249 [IOI 2014] Rail 铁路
题目背景
**仅支持 C++ 交互,请使用 C++17 或者更高语言版本提交。**
你不需要引入头文件,但请在代码头部加入如下内容:
```cpp
extern "C"
{
void findLocation(int n, int first, int location[], int stype[]);
int getDistance(int i, int j);
}
```
题目描述
台湾有一个连接着岛的东、西两岸的庞大的铁路线。这个铁路线包含有 $m$ 个区段。这些相连的区段以数字 $0, \dots, m - 1$ 为编号,且编号由西端开始。每一个区段都包含一段在北面向西单行的路轨,以及一段在南面向东单行的路轨。部分区段还可能会有一个位于这两段路轨之间的车站。
区段可以分成三种类型。其中 $C$ 类型的区段会有一个车站,而且只能从北面的路轨进入车站并且从南面的路轨离开。$D$ 类型的区段也会有一个车站,而且只能从南面的路轨进入车站并且从北面的路轨离开。空 类型的区段则没有车站。举例来说,如下图所示,区段 $0$、$4$ 和 $6$ 是空类型区段,区段 $1$、$2$ 和 $3$ 是 $C$ 类型,而区段 $5$ 则是 $D$ 类型。这些区段沿水平方向连接在一起。相邻区段的路轨之间以连接器彼此相连,在图中所示的灰色方块就是连接器。
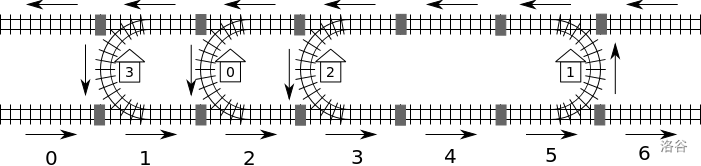
在这个铁路系统中共有 $n$ 个车站,它们分别以数字 $0$ 到 $n - 1$ 为编号。这里假设我们可以由任何一个车站出发、沿着路轨的方向到达任何其他车站。例如我们可以由车站 $0$ 到达车站 $2$,所经路线是由区段 $2$ 开始,经区段 $3$ 及区段 $4$ 的南面路轨,然后经由区段 $5$ 通过车站 $1$,再经区段 $4$ 的北面路轨,最后到达区段 $3$ 并由北面路轨进入车站 $2$。
由于从一个车站到另一个车站有多个不同的可行路线,我们定义由一个车站到另一个车站的距离为所有可行路线中所经的连接器的最少数量。例如由车站 $0$ 到车站 $2$ 的最短路线所经的区段是 $2 \rightarrow 3 \rightarrow 4 \rightarrow 5 \rightarrow 4 \rightarrow 3$,所经的连接器数目为 $5$,因此距离为 $5$。
该铁路系统是由计算机系统管理的。不幸的是,在一次电力事故后,计算机系统丢失了各车站所在的区段编号及其相应的类型。目前仅知道车站 $0$ 所在的区段编号,且该区段总是 $C$ 类型。幸运的是计算机能够查询出任意两个车站之间的距离。例如计算机可以查询“车站 $0$ 与车站 $2$ 的距离”,并且得到答案为 $5$。
### 任务
你需要编写一个函数 `findLocation`,以确定每一个车站所在的区段编号及其相应的类型。
- `findLocation(n, first, location, stype)`
- $n$:车站的数目
- $first$:车站 $0$ 所在区段的编号。
- $location$:大小为 $n$ 的数组;你需要将车站 $i$ 所在的区段编号存放到 $location[i]$ 中。
- $stype$:大小为 $n$ 的数组;你需要将车站 $i$ 的类型存放到 $stype[i]$ 中:其中 $1$ 表示 C 类型,而 $2$ 则表示 D 类型。
你可以调用一个函数 `getDistance` 以帮助你找出各车站的所在区段及其类型。
- `getDistance(i, j)` 将返回车站 $i$ 到车站 $j$ 的距离。如果调用 `getDistance(i, i)` 将返回 $0$。如果 $i$ 或 $j$ 在 $0 \leq i, j \leq n - 1$ 范围之外,`getDistance(i, j)` 将返回 $-1$。
### 子任务
在所有的子任务中,区段的数目 $m$ 不会超过 $1000000$。在部分子任务中,调用 `getDistance` 的次数是受限的,且该限制将因子任务而异。如果调用次数超过相应限制,你的程序将被判为“wrong answer”。
|子任务|分值 |$n$ |`getDistance` 的调用次数|备注 |
|:-:|:--:|:--------:|:--------:|:-:|
|$1$|$8$ |$1\le n\le 100$|无限制 |除车站 $0$ 外,其他车站均在 D 类型区段中。| |
|$2$|$22$|$1\le n\le 100$|无限制 |所有在车站 $0$ 东侧的车站均在 D 类型区段中,而所有在车站 $0$ 西侧的车站均在 C 类型区段中。| |
|$3$|$26$|$1\le n\le 5000$|$n(n-1)/2$|无其他限定 | |
|$4$|$44$|${1\le n\le 5000}$|$3(n-1)$ |无其他限定 | |
### 实现细节
**本题只支持 C/C++。**
你只能提交一个源文件实现如上所述的 `findLocation` 函数,并且遵循下面的命名和接口。
```cpp
void findLocation(int n, int first, int location[], int stype[]);
```
函数 `getDistance` 的接口信息如下。
```cpp
int getDistance(int i, int j);
```
#### 评测方式
下面为下发文件的介绍。
评测系统将读入如下格式的输入数据:
1. 第 $1$ 行:子任务编号。
2. 第 $2$ 行:$n$。
3. 第 $3+i$ 行:$stype[i]$($1$ 表示 $C$ 类型,$2$ 表示 $D$ 类型),$location[i]$($0 \leq i \leq n - 1$)。
在 `findLocation` 返回后,如果你的程序计算出的 $location[0],\dots,location[n-1]$ 和 $stype[0],\dots,stype[n-1]$ 与输入数据一致,评测系统将输出 $\texttt{Correct}$,否则输出 $\texttt{Incorrect}$。
输入格式
无
输出格式
无
说明/提示
本题实际评测时使用的交互库与下发文件不同(增加了一些反作弊)。