P15271 [Google Hashcode 2022 Finals] Santa Tracker
题目背景
自 2004 年起,[**Google Santa Tracker**](https://santatracker.google.com/) 项目每年都会帮助可视化传奇人物圣诞老人在每年十二月为世界各地孩子们分发礼物所采取的路线。
尽管距离十二月还有几个月,但在拉普兰的圣诞老人家里,准备工作正在如火如荼地进行。Google Santa Tracker 也在准备中,有传言称今年将会格外有趣。一个由光速飞行工程师(ELF)组成的秘密团队,与拉普兰的慷慨礼物物流工程地精研究所(GIGGLE)合作,正在开发新的实验性优化算法,以帮助圣诞老人更有效地递送礼物。
早期结果很有希望,但圣诞老人认为它们可以改进。当圣诞老人了解到 Hash Code 参与者著名的优化技能时,他询问 Hash Code 世界总决赛选手是否能够提供帮助。**你准备好接受挑战了吗?**
---
#### 任务
圣诞老人正在一个无摩擦的二维平面上递送礼物,使用由驯鹿驱动的雪橇,并依靠……胡萝卜 🥕 来加速。
你的任务是规划雪橇的行动,以递送礼物并最大化总得分。
题目描述
#### 世界
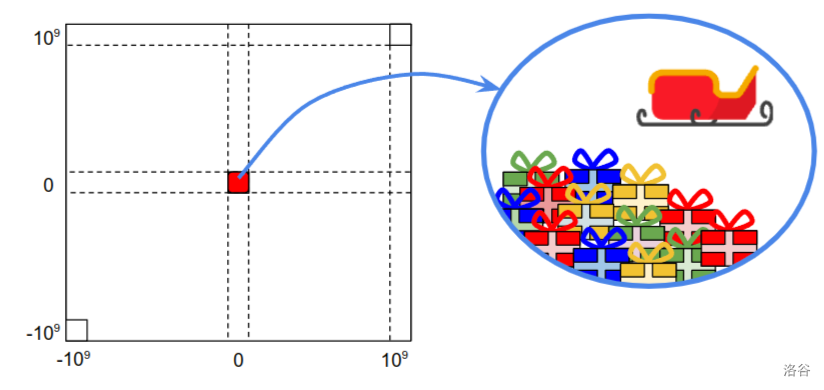
世界是一个具有整数坐标的二维网格。我们将第 $c$ 列、第 $r$ 行的单元格称为 $(c, r)$ ($-10^9 \leq c, r \leq 10^9$)。
两个单元格 $(c_a, r_a)$ 和 $(c_b, r_b)$ 之间的**距离**计算为 $\sqrt{|c_a - c_b|^2 + |r_a - r_b|^2}$(欧几里得距离)。
圣诞老人从拉普兰 $(0, 0)$ 出发,那里存放着所有的礼物。
:::align{center}
:::
圣诞老人只有 $T$ 秒的时间来递送礼物,所以请抓紧时间!
#### 礼物和胡萝卜
圣诞老人可以装载到雪橇上的物品有两种:礼物和胡萝卜。
**礼物**需要递送给世界各地的孩子们。你被给予 $G$ 个礼物的列表,对于每个礼物,你知道:
- 应收到礼物的孩子的名字,
- 递送此礼物所奖励的得分,
- 礼物的重量(以千克为单位),
- 需要递送的坐标 $(c, r)$。
**胡萝卜**是圣诞老人的神奇驯鹿的食物,它们需要吃掉胡萝卜来加速。每根胡萝卜重 $1$ 千克(是的,我们知道它们很重……但它们确实很神奇!)。
得益于一支非常高效的助手地精团队,礼物递送在每秒钟开始时瞬间完成。同样,礼物/胡萝卜装载也在每秒钟开始时瞬间完成。
#### 范围
圣诞老人可以向距离他的雪橇最大距离 $D$(包括 $D$)内的所有孩子递送礼物。同样,只要雪橇距离其基地 $(0, 0)$ 的最大距离在 $D$(包括 $D$)内,圣诞老人就可以装载礼物和胡萝卜。我们称这个最大距离 $D$ 为“范围”。
::::info[例如:]
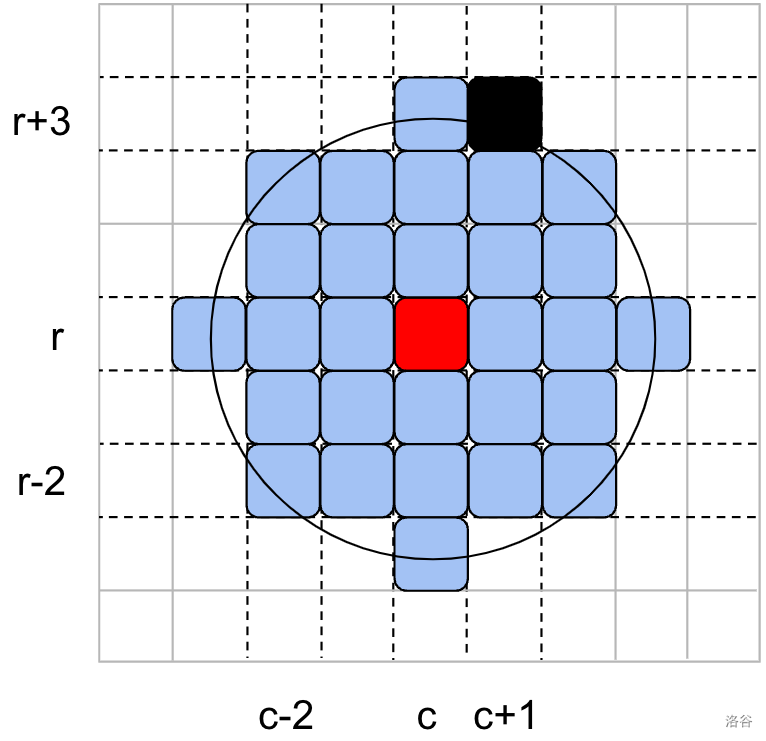
例如,对于范围 $D = 3$ 和雪橇在 $(c, r)$:
- 单元格 $(c - 2, r - 2)$ 在 $(c, r)$ 的范围内,因为欧几里得距离为 $\sqrt{|(c - 2) - c|^2 + |(r - 2) - r|^2} = \sqrt{8}$ 且 $\sqrt{8} \leq 3$。
- 单元格 $(c + 1, r + 3)$(下图中标记为黑色)**不在** $(c, r)$ 的范围内,因为欧几里得距离为 $\sqrt{|(c + 1) - c|^2 + |(r + 3) - r|^2} = \sqrt{10}$ 且 $\sqrt{10} > 3$。
:::align{center}
:::
::::
#### 导航
圣诞老人乘坐他的神奇雪橇在世界中移动。
得益于雪橇上的魔法涂层,圣诞老人不会遇到摩擦,并且可以无限期地保持速度。在任何时候,雪橇的运动可以用其速度 $[s_c, s_r]$ 来描述,表示雪橇每秒在每个方向上移动的速度。
圣诞老人以速度 $[0, 0]$(静止)开始。
::::info[例如:]
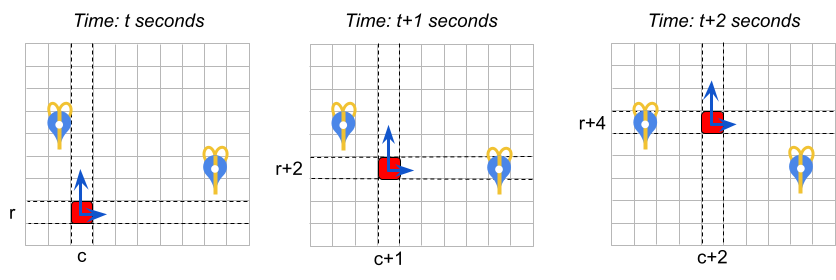
例如,在下图中,雪橇初始位置为 $(c, r)$,其速度为 $[1, 2]$。
只要速度保持不变,每秒后雪橇将向右移动 1 个位置,向上移动 2 个位置。
:::align{center}
:::
::::
#### 机动
每秒,圣诞老人可以选择将一根胡萝卜(先前装载到雪橇上)喂给驯鹿,以在四个方向之一(上、下、左、右)按选定值加速。“加速”意味着改变速度。如果初始速度为 $[s_c, s_r]$ 并且圣诞老人加速,那么:
- “向上加速” $a$ 意味着将速度改变为 $[s_c, s_r + a]$
- “向下加速” $a$ 意味着将速度改变为 $[s_c, s_r - a]$
- “向右加速” $a$ 意味着将速度改变为 $[s_c + a, s_r]$
- “向左加速” $a$ 意味着将速度改变为 $[s_c - a, s_r]$
注意,“加速”(如上定义)的概念也允许圣诞老人“减速”。例如,如果向上加速 2 使圣诞老人的雪橇走得更快,那么随后向下“加速” 2 会使他们走得更慢。
圣诞老人可以选择加速,但即使是神奇雪橇也有其局限性!圣诞老人的驯鹿在给定时刻能提供的最大加速度取决于雪橇的当前重量。雪橇越重,最大加速度越慢!
雪橇的重量是以下各项之和:
- 装载在雪橇上的礼物的重量
- 装载在雪橇上的胡萝卜的重量
每个输入数据集指定了在给定雪橇重量范围内的**最大加速度**。对于雪橇重量范围 $(l_{i-1}, l_i]$ 的最大加速度 $a_i$ 意味着,对于所有满足 $l_{i-1} < w \leq l_i$ 约束的雪橇重量 $w$,最大加速度等于 $a_i$(包括边界)。
上述雪橇重量包括即将被驯鹿吃掉的胡萝卜。然而,在加速之后,胡萝卜立即被吃掉并转化为驯鹿能量,瞬间将雪橇重量减少 $1$ 千克。
如果驯鹿无法承受雪橇的重量($w$ 超过最大 $l_i$),它们**根本无法加速**(最大加速度 = 0)。雪橇保持其速度并继续漂浮,直到再次可能加速(例如礼物被递送)或时间用完。此外,如果雪橇上没有胡萝卜,则无法加速!
加速是瞬间发生的,发生在每秒钟开始时。圣诞老人的雪橇每秒只能加速一次(在另一次加速之前必须至少漂浮一秒)。
考虑下面描述和图中所示的示例。
加速度范围如下,对于雪橇重量 $w$:
- 如果 $0 < w \leq 30$ 千克,雪橇最多可以加速 4
- 如果 $30$ 千克 $< w \leq 500$ 千克,雪橇最多可以加速 2
- 如果重量高于 500 千克,雪橇根本无法加速
::::info[例如:]
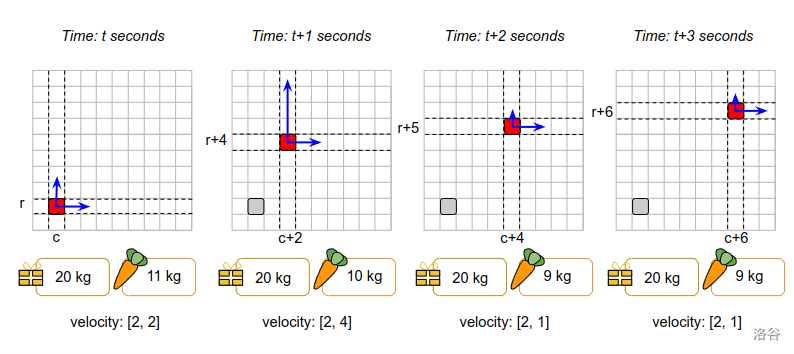
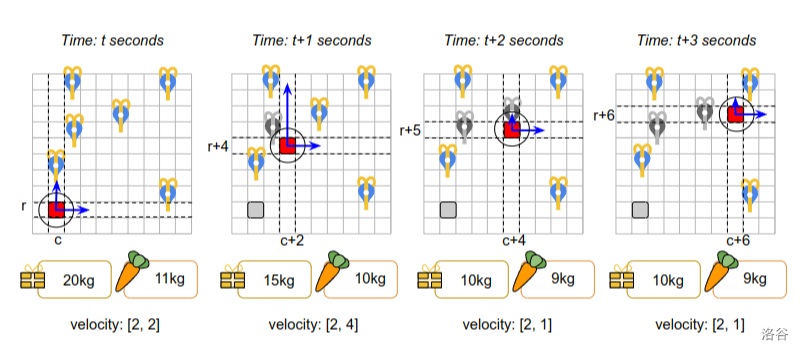
雪橇的初始重量包括 20 千克礼物和 11 千克胡萝卜。所以总重量为 31 千克,这意味着最大加速度为 2。在 $t$ 秒时的初始速度为 $[2, 2]$。
- 在 $t$ 秒时:雪橇位于 $(c, r)$。雪橇向上加速 2(这是雪橇重量为 31 千克时允许的最大加速度)。由于加速发生在该秒开始时,$t$ 秒开始时的新的速度为 $[2, 4]$。因为使用了一根胡萝卜,雪橇重量变为 30 千克。然后雪橇漂浮 1 秒。
- 在 $t + 1$ 秒时:雪橇位于 $(c + 2, r + 4)$。雪橇向下加速 3(现在允许,因为上一秒重量减少到 30 千克,最大加速度增加到 4)。$t + 1$ 秒开始时的新的速度为 $[2, 1]$。然后雪橇漂浮 1 秒。
- 在 $t + 2$ 秒时:雪橇位于 $(c + 4, r + 5)$。雪橇不加速(速度保持为 $[2, 1]$)并再漂浮一秒。
- 在 $t + 3$ 秒时:雪橇位于 $(c + 6, r + 6)$
:::align{center}
:::
::::
注意,当礼物递送给孩子们时,雪橇的重量也会更新。
::::info[例如:]
考虑下面的例子。雪橇移动与上图相同,但我们增加了礼物递送。范围为 $D = 1$。
- 在 $t + 1$ 秒时:雪橇位于 $(c + 2, r + 4)$。我们递送一个礼物到单元格 $(c + 1, r + 4)$,将雪橇重量减少 5 千克。
- 在 $t + 2$ 秒时:雪橇位于 $(c + 4, r + 5)$。我们递送一个礼物到单元格 $(c + 4, r + 5)$(雪橇所在的同一单元格),将雪橇重量再减少 5 千克。
观察到,尽管在 $t$ 和 $t + 1$ 之间雪橇经过了礼物递送位置 $(c, r + 2)$ 附近,但不可能递送它。这是因为礼物递送必须发生在每秒开始时,而不是在雪橇漂浮时。
:::align{center}
:::
::::
#### 行动
雪橇可以执行以下行动。除“漂浮”外的所有行动都是瞬间的(花费 0 秒)。无论雪橇是否在移动,都可以执行所有行动(无需停止来递送或装载雪橇)。
- **加速** 沿四个方向之一(上、下、左或右)按给定加速度加速(不超过雪橇当前重量允许的最大加速度)。在两次连续加速之间,雪橇必须至少执行一次漂浮行动。
- **漂浮** 若干秒。在漂浮行动期间,雪橇的速度保持恒定。
- **装载若干根胡萝卜**。雪橇需要距离初始位置 $(0, 0)$ 在 $D$ 的距离内。
- **装载一个给定的礼物**。雪橇需要距离初始位置 $(0, 0)$ 在 $D$ 的距离内。
- **递送一个给定的礼物**。给定礼物的递送位置需要距离雪橇的位置在 $D$ 的距离内。
:::info[例如:]
例如,以下 3 个行动序列是有效的:
1. 向上加速 → 漂浮 → 向下加速 → 漂浮
2. 向上加速 → 递送礼物 → 漂浮 → 装载胡萝卜 → 漂浮 → 向左加速 → 漂浮
3. 漂浮 → 向上加速
注意,在(3)中,最后的“向上加速”行动不影响雪橇的最终位置:速度被更新,但在发出“漂浮”命令之前,雪橇不会以更新后的速度移动。
以下 2 个行动序列无效,因为两次加速行动之间没有任何漂浮行动:
- ❌ 向左加速 → 向下加速 → 漂浮
- ❌ 漂浮 → 向上加速 → 装载胡萝卜 → 向下加速
:::
输入格式
输入数据 [完整输入(压缩)](https://www.luogu.com.cn/fe/api/problem/downloadAttachment/e4rrlxb4)
每个输入数据集以纯文本文件提供。文件仅包含 ASCII 字符,行以单个 '\n' 字符(也称为“UNIX 风格”行结尾)结束。当一行中给出多个字符串和数字时,它们之间用单个空格分隔。
输入文件的第一行包含:
- $T$ - 时间限制(以秒为单位),($1 \leq T \leq 10,000$)
- $D$ - 可达范围 ($0 \leq D \leq 100$),即礼物递送和礼物/胡萝卜装载的最大距离
- $W$ - 雪橇的加速度范围数量 ($1 \leq W \leq 10$)
- $G$ - 数据集中的礼物数量,($1 \leq G \leq 10,000$)
随后的 $W$ 行包含加速度范围描述——两个由单个空格分隔的整数:
- $l_i$ - 一个整数,使用以下加速度的最大雪橇重量 ($1 \leq l_i \leq 10^6$)
- $a_i$ - 一个整数,此加速度范围的最大加速度 ($1 \leq a_i \leq 100$)
注意,雪橇对于最大加速度 $a_i$ 的重量范围是 $[l_{i-1}, l_i]$,其中 $l_0 = 0$。保证 $l_{i-1} < l_i$ 且 $a_{i-1} > a_i$
随后的 $G$ 行包含礼物描述——由单个空格分隔的字符串和整数:
- $name_i$ - 孩子的名字(唯一的字符串,由最多 30 个字符的 a-z、A-Z、0-9 字符组成)
- $s_i$ - 一个整数,递送礼物的得分 ($1 \leq s_i \leq 10,000$)
- $w_i$ - 一个整数,礼物的重量(以千克为单位)($1 \leq w_i \leq 1,000$)
- $c_i$ - 孩子位置的列 ($-10^9 \leq c_i \leq 10^9$)
- $r_i$ - 孩子位置的行 ($-10^9 \leq r_i \leq 10^9$)
保证数据集中的每个位置 $(c_i, r_i)$ 最多有一个礼物接收者,并且保证拉普兰 $(0, 0)$ 没有礼物接收者。
输出格式
你需要指定圣诞老人的行动。
#### 文件格式
提交文件必须是纯文本文件,仅包含以单个 '\n' 字符(“UNIX 风格”行结尾)结尾的 ASCII 字符行。
第一行必须包含一个整数 $C$ ($0 \leq C \leq 10^6$):圣诞老人的行动数量。
随后的每一行必须包含雪橇的一个有效行动。每个行动描述必须包含行动名称和行动参数,由空格分隔。可能的行动有:
- **AccUp (a)** - 以整数 $a$ ($0 \leq a \leq a_i$,其中 $a_i$ 是雪橇当前重量适用的最大加速度)沿“上”方向加速
- **AccDown (a)** - 以整数 $a$ ($0 \leq a \leq a_i$,其中 $a_i$ 是雪橇当前重量适用的最大加速度)沿“下”方向加速
- **AccLeft (a)** - 以整数 $a$ ($0 \leq a \leq a_i$,其中 $a_i$ 是雪橇当前重量适用的最大加速度)沿“左”方向加速
- **AccRight (a)** - 以整数 $a$ ($0 \leq a \leq a_i$,其中 $a_i$ 是雪橇当前重量适用的最大加速度)沿“右”方向加速
- **Float (t)** - 将时间推进整数 $t$ 秒 ($1 \leq t \leq T$)。在每一秒中,雪橇的位置以当前速度前进。
- **LoadCarrots (N)** - 将整数 $N$ 根胡萝卜装载到雪橇上 ($1 \leq N \leq 1,000,000$),仅在距离 $(0, 0)$ 在 $D$ 距离内(包括 $D$)有效。
- **LoadGift (ChildName)** - 装载给指定孩子的礼物,仅在距离 $(0, 0)$ 在 $D$ 距离内(包括 $D$)有效。
- **DeliverGift (ChildName)** - 递送给指定孩子的礼物,仅在距离该孩子在 $D$ 距离内(包括 $D$)有效。
说明/提示
#### 示例
| 输入文件 | 描述 |
|:-:|:-:|
| `15 3 4 4` | 15 秒,递送距离为 3,4 个加速度范围和 4 个礼物 |
| `15 8` | 对于重量从 0 到 15,最大加速度为 8 |
| `30 6` | 对于重量从 16 到 30,最大加速度为 6 |
| `45 4` | 对于重量从 31 到 45,最大加速度为 4 |
| `60 2` | 对于重量从 46 到 60,最大加速度为 2(对于重量大于 60 千克,最大加速度为 0) |
| `Olivia 1 10 5 1` | 给 Olivia 的礼物,得分 1,10 千克,位于 (5, 1) |
| `Emma 2 10 -10 1` | 给 Emma 的礼物,得分 2,10 千克,位于 (-10, 1) |
| `Liam 5 10 8 4` | 给 Liam 的礼物,得分 5,10 千克,位于 (8, 4) |
| `Bob 10 15 0 -100` | 给 Bob 的礼物,得分 10,15 千克,位于 (0, -100) |
**注意,输入文件不包含任何空行。上例中的空行和换行是为了清晰而添加的。**
| 提交文件 | 描述 |
|:-:|:-:|
| `23` | 文件描述了 23 个行动 |
| `LoadCarrots 10` | 装载 10 根胡萝卜,重量增加到 10 千克 |
| `LoadGift Olivia` | 装载 Olivia 的礼物,重量增加到 20 千克 |
| `LoadGift Liam` | 装载 Liam 的礼物,重量增加到 30 千克。现在最大加速度为 6 |
| `AccRight 4` | 加速,将速度改变为 $[4,0]$,重量变为 29 千克 |
| `Float 1` | 让 1 秒过去。圣诞老人移动到 $(4,0)$ |
| `DeliverGift Olivia` | 递送给 Olivia 的礼物,重量减少到 19 千克 |
| `AccUp 2` | 加速,将速度改变为 $[4,2]$,重量变为 18 千克 |
| `Float 1` | 让 1 秒过去。圣诞老人移动到 $(8,2)$ |
| `DeliverGift Liam` | 递送给 Liam 的礼物,重量减少到 8 千克。现在最大加速度为 8 |
| `AccLeft 8` | 加速,将速度改变为 $[-4,2]$,重量变为 7 千克 |
| `Float 1` | 让 1 秒过去。圣诞老人移动到 $(4,4)$ |
| `AccDown 4` | 加速,将速度改变为 $[-4,-2]$,重量变为 6 千克 |
| `Float 1` | 让 1 秒过去。圣诞老人移动到 $(0,2)$ |
| `LoadGift Bob` | 装载 Bob 的礼物,重量增加到 21 千克。现在最大加速度为 6 |
| `AccRight 4` | 加速,将速度改变为 $[0,-2]$,重量变为 20 千克 |
| `Float 1` | 让 1 秒过去。圣诞老人移动到 $(0,0)$ |
| `AccDown 6` | 加速,将速度改变为 $[0,-8]$,重量变为 19 千克 |
| `Float 1` | 让 1 秒过去。圣诞老人移动到 $(0,-8)$ |
| `AccDown 6` | 加速,将速度改变为 $[0,-14]$,重量变为 18 千克 |
| `Float 1` | 让 1 秒过去。圣诞老人移动到 $(0,-22)$ |
| `AccDown 6` | 加速,将速度改变为 $[0,-20]$,重量变为 17 千克 |
| `Float 4` | 让 4 秒过去。圣诞老人移动到 $(0,-102)$ |
| `DeliverGift Bob` | 递送给 Bob 的礼物,重量减少到 2 千克 |
**注意,提交文件不应包含任何空行。上例中的空行和换行是为了清晰而添加的。**
#### 验证
为了使提交被接受,必须满足以下条件:
- ⚠️ 提交文件必须恰好有 $C + 1$ 行,格式如上所述。
- ⚠️ 当圣诞老人距离 $(0, 0)$ 超过 $D$ 时,不得尝试将礼物或胡萝卜装载到雪橇上。
- ⚠️ 当圣诞老人距离目的地超过 $D$ 时,不得尝试递送礼物。
- ⚠️ 圣诞老人只能递送每个礼物一次,并且只有在它先前被装载到雪橇上时。
- ⚠️ 圣诞老人只能装载每个礼物一次。(礼物被装载后,要么被递送,要么留在雪橇上直到模拟结束。)
- ⚠️ 圣诞老人不得尝试超过雪橇当前重量允许的最大加速度进行加速。
- ⚠️ 圣诞老人不得尝试在一秒内加速超过一次(中间没有**漂浮**行动)。
- ⚠️ 圣诞老人不得在模拟时间用完后尝试**漂浮**行动。
#### 评分
你的解决方案的得分是每个已递送礼物所奖励的得分之和。
> 例如,示例解决方案得分为 $16$ 分:Olivia 的礼物 $1$ 分,Liam 的礼物 $5$ 分,Bob 的礼物 $10$ 分。
注意,有多个数据集代表问题的单独实例。你团队的最终得分将是各个数据集上最佳得分的总和。
你需要在本题中获得总共不低于 1300000 分,才可以被视作通过本题。赛场上的最高分是 5396369 分。
翻译由 DeepSeek 完成