P15272 [Google Hashcode 2021 Qualification] Traffic signaling

#### 介绍 世界上第一个交通信号灯可以追溯到 1868 年。它被安装在伦敦，用于控制……马车的交通！如今，交通信号灯几乎可以在世界每个城市的街道交叉口找到，使车辆更安全地通过。 交通信号灯至少有两种状态，使用一种颜色（通常是红色）表示“停止”，另一种颜色（通常是绿色）表示车辆可以通行。最早的交通信号灯是手动控制的。如今它们是自动的，这意味着必须仔细设计和定时，以优化所有交通参与者的总通行时间。 #### 任务 给定一个城市规划的描述以及该城市中所有车辆的规划路径，优化交通信号灯的调度，以最小化在交通中花费的总时间，并帮助尽可能多的车辆在给定的截止时间前到达目的地。

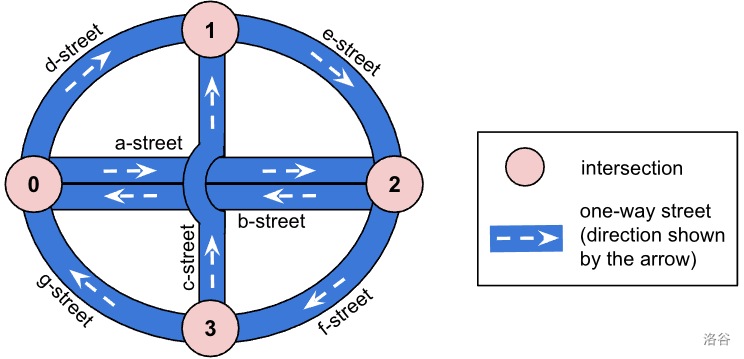
#### 城市规划 城市规划包括单向街道和交叉口。每条街道： - 由一个唯一的名称标识， - 从一个交叉口通向另一个交叉口， - 中间不包含任何交叉口（如果两条街道需要在交叉口外交叉，则使用桥梁或隧道）， - 有一个固定的时间 $L$，表示一辆车从街道起点到终点所需的时间。如果一条街道的通行时间为 $L$ 秒，一辆车在时间 $T$ 进入该街道，那么它将在 $T + L$ 时刻精确到达街道终点，与街道上有多少车辆无关。 :::align{center}  ::: 图 1. 一个包含 4 个交叉口（0、1、2 和 3）和 7 条街道（a、b、……、g 街）的城市规划。 交叉口 0 和 2 通过 a 街和 b 街双向直接连接。c 街使用一座桥梁跨越 a 街和 b 街，不与这两条街道相交。 注意，虽然街道是单向的，但仍然可能有两个单向街道以相反方向连接两个交叉口（见图 1 中的交叉口 0 和 2 以及 a 街和 b 街）。但是，永远不会有两条街道以相同方向连接两个交叉口。 #### 每个交叉口： - 有一个唯一的整数 ID（例如 $0, 1, 2, \ldots$）， - 至少有一条街道进入它，并且至少有一条街道从它引出。 #### 交通信号灯 每条街道的终点（紧邻交叉口前）都有一个交通信号灯。每个交通信号灯有两种状态：绿灯表示该街道的车辆可以穿过交叉口并前往任何其他街道，红灯表示该街道的车辆需要停止。在任何给定时间，每个交叉口最多有一个交通信号灯是绿灯。当进入街道的绿灯亮起时，只有来自该街道的车辆被允许进入交叉口（并移动到任何引出街道），所有其他车辆必须等待。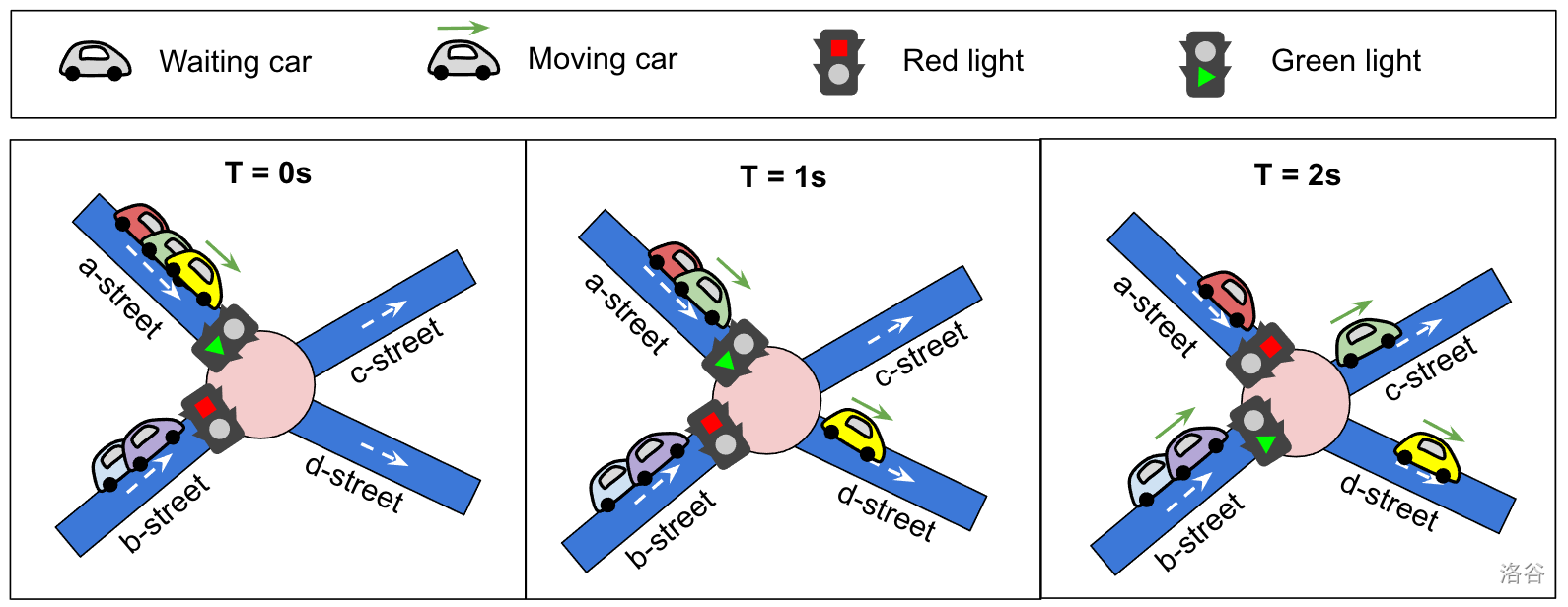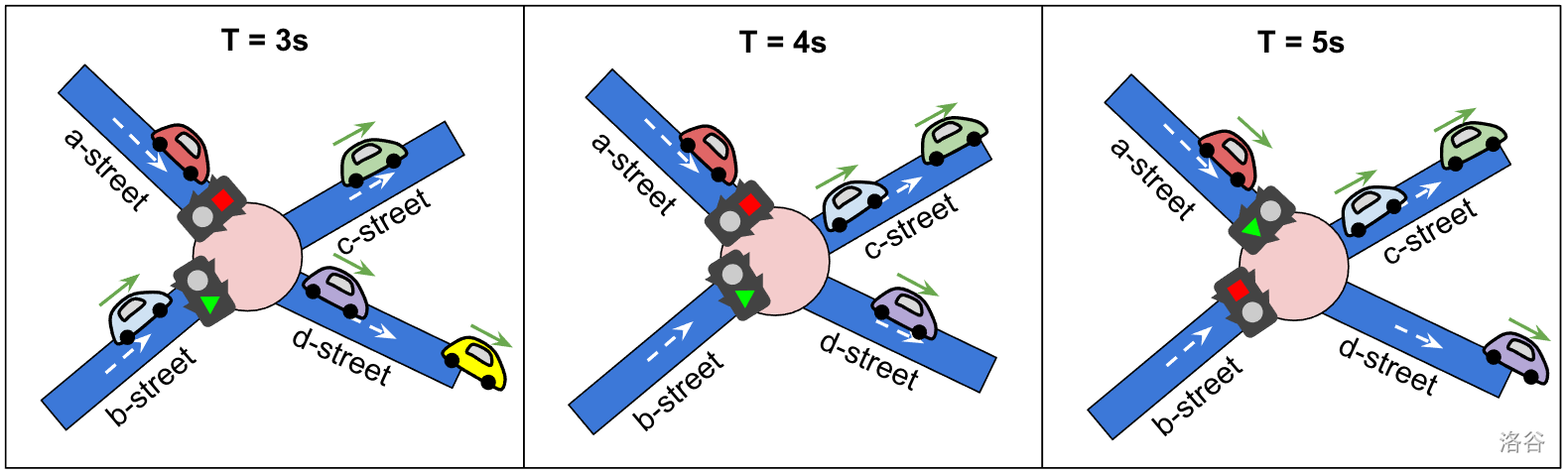 ##### 排队 当街道终点的信号灯为红色时，到达的车辆排队等待绿灯。**当绿灯亮起时，每秒可以有一辆车通过交叉口。** 这意味着，如果给定街道的绿灯持续 $T_i$ 秒，那么只有该街道的前 $T_i$ 辆车将继续行驶（见图 2）。其他车辆需要等待下一个绿灯。 :::align{center}   ::: 图 2. 考虑一个具有两条进入街道（a 街有 3 辆等待车辆，b 街有 2 辆等待车辆）和两条引出街道（c 街和 d 街）的交叉口。有两个交通信号灯，一个在 a 街终点，$T_1 = 2$；一个在 b 街终点，$T_2 = 3$。最初，a 街的信号灯是绿灯，第一辆（黄色）车开始移动。在 $T = 1$ 时，a 街的下一辆（绿色）车开始移动。在 $T = 2$ 时，a 街变为红灯，最后一辆（红色）等待的车辆需要停止。同时，b 街的信号灯变为绿灯，第一辆（紫色）排队车辆开始移动。在 $T = 3$ 和 $T = 4$ 时，最初在 b 街上的两辆（紫色和蓝色）车已经通过了信号灯并继续行驶。在 $T = 5$ 时，a 街的信号灯再次变为绿灯，等待的（红色）车现在可以移动。 ##### 调度 对于每个交叉口，我们可以设置一个交通信号灯调度。交通信号灯调度决定了该交叉口进入街道绿灯的顺序和持续时间，并重复直到模拟结束。调度是一个配对列表：进入街道和持续时间。**每条街道在调度中最多出现一次。** 调度可以忽略一些进入街道——那些街道将永远不会获得绿灯。 交通信号灯调度由你的提交控制。你不必指定所有交通信号灯的调度。**默认情况下，所有交叉口的所有信号灯都是红色的**（是的，被困在那里的车辆将不得不等待直到模拟结束）。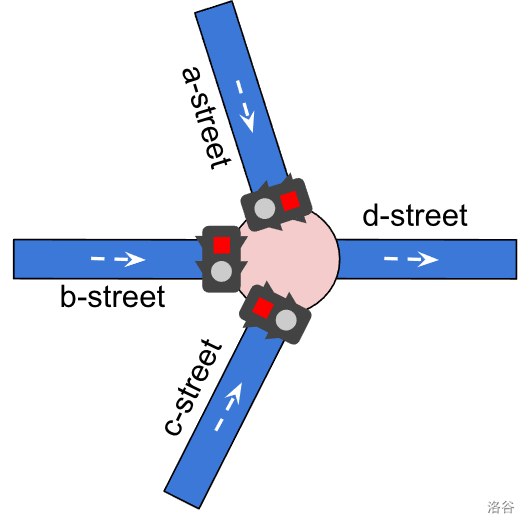 ##### 交通信号灯调度示例 在以下示例中，一个交叉口有 3 条街道通向它（a、b 和 c 街），以及一条离开交叉口的街道（d 街）。我们考虑这些交通信号灯的三种不同调度示例： **无交通信号灯调度（默认）。** :::align{center}  ::: 图 4（a）。如果没有为交叉口设置交通信号灯调度，所有信号灯在整个模拟期间保持红色。任何计划通过 a、b 或 c 街的车辆将被阻塞，无法到达目的地。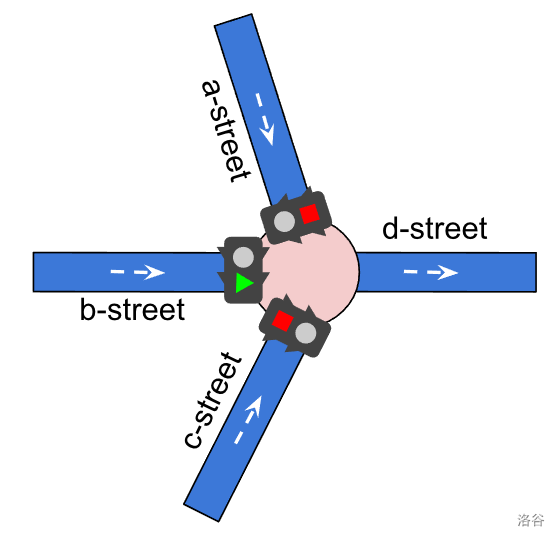 **仅覆盖一条街道的调度。** :::align{center}  ::: 图 4（b）。在此示例中，交通信号灯调度仅覆盖一条进入街道（b 街）。在这种情况下，b 街始终是绿灯。任何来自 b 街的车辆将总是直接通过交叉口，而任何计划通过 a 街或 c 街的车辆将被阻塞，无法到达目的地。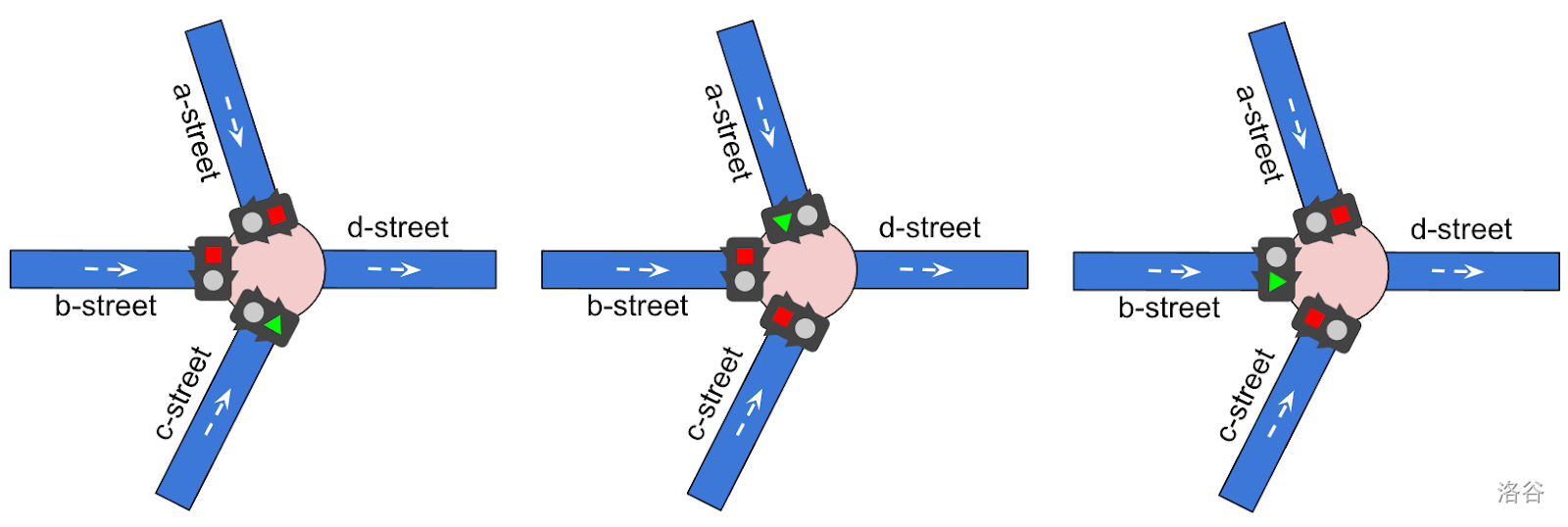 **覆盖所有街道的调度。** :::align{center}  ::: 图 4（c）。在此示例中，交通信号灯调度覆盖所有进入街道（先是 c 街，然后是 a 街，然后是 b 街）。对于每条街道，我们可以定义不同的 $T_i$，意味着该信号灯保持绿灯的不同持续时间。 #### 车辆 每辆车由其行驶的路径（街道序列）描述。路径由输入数据集定义且不可更改。在输入数据集中，我们保证每辆车最多通过同一个交叉口一次。 最初，所有车辆从它们路径中第一条街道的**终点**开始，等待绿灯（如果信号灯是红色），或准备移动（如果是绿灯）。如果两辆车从同一条街道的终点开始，输入文件中列出的第一辆车先行。然后每辆车遵循给定路径，同时遵守交通信号灯，并需要到达该路径中最后一条街道的终点。 车辆在每条街道的终点排队。队列中的第一辆车可以在绿灯亮起后立即通过交叉口。车辆通过交叉口时没有延迟。之后的车辆**每秒一辆**依次通过交叉口。 当一辆车进入其路径的最后一条街道时，它会一直行驶到该街道的终点，然后**立即被移除**。这意味着该车不会在其路径的最后一条街道终点排队，也不会进入其终点的交叉口。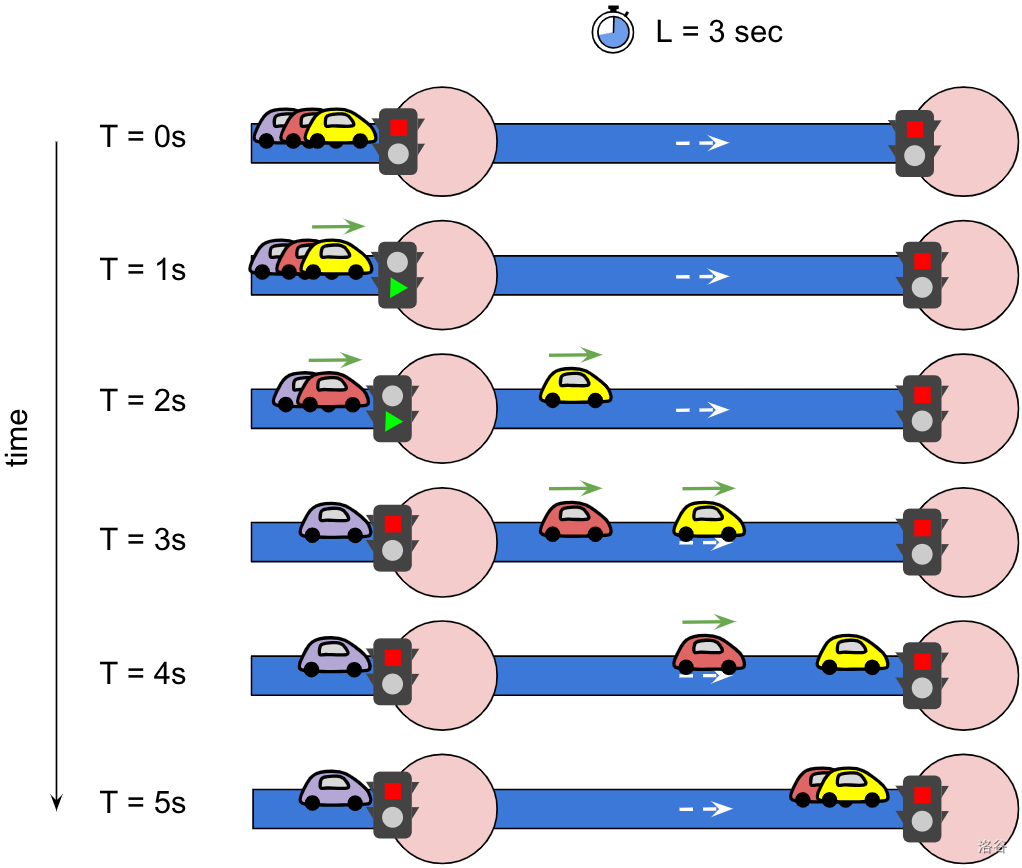 :::align{center}  ::: 图 3. 此图显示了在精确 $T$ 秒时三辆车的状态，模拟从 $T = 0$ 开始，到 $T = 5$ 结束。街道的 $L = 3$，意味着任何车辆需要 3 秒从其起点到终点。左侧交叉口的绿灯在 $T = 1$ 时亮起，并在 2 秒后再次变红。车辆在街道终点排队，黄色车是第一辆。在 $T = 1$ 时，**第一辆（黄色）车**立即开始移动，并在 3 秒后，即 $T = 4$ 时到达街道终点。**第二辆（红色）车**必须等待 1 秒才能开始移动，并在 3 秒后，即 $T = 5$ 时到达街道终点。**第三辆（紫色）车**没有足够时间进入街道，因为信号灯已经变红。注意，为简单起见，此图仅显示两条街道：当显示信号灯为红色时，这意味着同一交叉口中的另一个信号灯变为绿灯。

输入数据 [完整输入（压缩）](https://www.luogu.com.cn/fe/api/problem/downloadAttachment/n6569k3b) #### 文件格式 每个输入数据集以纯文本文件提供。文件仅包含 ASCII 字符，行以单个 `\n` 字符（也称为“UNIX 风格”行结尾）结束。当一行中给出多个数字时，它们之间用单个空格分隔。 第一行包含五个数字： - 一个整数 $D$ ($1 \leq D \leq 10^4$) - 模拟的持续时间，以秒为单位， - 一个整数 $I$ ($2 \leq I \leq 10^5$) - 交叉口的数量（ID 从 0 到 $I - 1$）， - 一个整数 $S$ ($2 \leq S \leq 10^5$) - 街道的数量， - 一个整数 $V$ ($1 \leq V \leq 10^3$) - 车辆的数量， - 一个整数 $F$ ($1 \leq F \leq 10^3$) - 每辆车在时间 $D$ 前到达目的地所获得的奖励分数。 接下来的 $S$ 行包含街道的描述。每行包含： - 两个整数 $B$ ($0 \leq B < I$) 和 $E$ ($0 \leq E < D$) - 分别是街道起点和终点的交叉口， - 街道名称（一个由 3 到 30 个小写 ASCII 字符 a-z 和字符 - 组成的字符串）， - 一个整数 $L$ ($1 \leq L \leq D$) - 一辆车从该街道起点到终点所需的时间。 接下来的 $V$ 行描述每辆车的路径。每行包含： - 一个整数 $P$ ($2 \leq P \leq 10^3$) - 车辆想要行驶的街道数量， - 后跟 $P$ 个街道名称：**车辆从第一条街道的终点开始**（即它等待绿灯以移动到下一条街道），并沿着路径直到最后一条街道的终点。车辆的路径总是有效的，即街道将通过交叉口连接。

你的提交描述了你想要为特定交叉口设置的交通信号灯调度。 #### 文件格式 第一行必须包含一个整数 $A$ ($0 \leq A \leq I$)，即你指定调度的交叉口数量。 然后，提交文件必须以任意顺序描述交叉口调度。每个调度必须由多行描述： - 第一行包含一个整数 $i$ ($0 \leq i < I$) – 交叉口的 ID， - 第二行包含一个整数 $E_i$ ($0 < E_i$) – 此调度覆盖的进入街道（属于交叉口 $i$）的数量， - $E_i$ 行描述绿灯的顺序和持续时间。每行必须包含（由单个空格分隔）： - 街道名称， - 一个整数 $T$ ($1 \leq T \leq D$) 表示每条街道绿灯将持续的时间。 每个交叉口在提交文件中只能列出一次。并且每个街道名称在每个调度中只能列出一次。如果街道名称未出现在交叉口配置中，则其信号灯始终为红色。如果交叉口配置未出现在提交文件中，则其所有信号灯始终为红色。

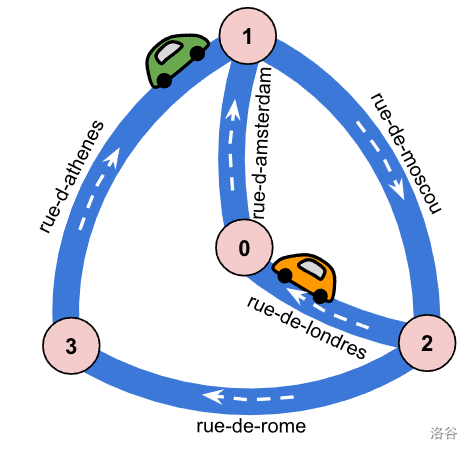
#### 示例 | 输入文件 | 描述 | |:-:|:-:| | `6 4 5 2 1000` | 6 秒，4 个交叉口，5 条街道，2 辆车，准时到达目的地奖励 1000 分。 | | `2 0 rue-de-londres 1` | 街道 `rue-de-londres` 从交叉口 2 开始，到 0 结束，且 $L=1$。 | | `0 1 rue-d-amsterdam 1` | 街道 `rue-d-amsterdam` 从交叉口 0 开始，到 1 结束，且 $L=1$。 | | `3 1 rue-d-athenes 1` | 街道 `rue-d-athenes` 从交叉口 3 开始，到 1 结束，且 $L=1$。 | | `2 3 rue-de-rome 2` | 街道 `rue-de-rome` 从交叉口 2 开始，到 3 结束，且 $L=2$。 | | `1 2 rue-de-moscou 3` | 街道 `rue-de-moscou` 从交叉口 1 开始，到 2 结束，且 $L=3$。 | | `4 rue-de-londres rue-d-amsterdam rue-de-moscou rue-de-rome` | 第一辆车从 `rue-de-londres` 的终点开始，然后遵循给定路径。 | | `3 rue-d-athenes rue-de-moscou rue-de-londres` | 第二辆车从 `rue-d-athenes` 的终点开始，然后遵循给定路径。 | :::align{center}  ::: | 提交文件 | 描述 | |:-:|:-:| | `3` | 有 3 个交叉口设有交通信号灯调度： | | `1` | 在交叉口 1，交通信号灯对以下街道为绿灯 | | `2` | 2 条不同的进入街道，即 | | `rue-d-athenes 2` | `rue-d-athenes` 绿灯 2 秒，然后 | | `rue-d-amsterdam 1` | `rue-d-amsterdam` 绿灯 1 秒，然后再回到 `rue-d-athenes`。 | | `0` | 在交叉口 0，交通信号灯对 | | `1` | 仅 1 条进入街道为绿灯，即 | | `rue-de-londres 2` | `rue-de-londres` 每周期绿灯 2 秒（对 `rue-de-londres` 始终为绿灯）。 | | `2` | 在交叉口 2，交通信号灯对 | | `1` | 仅 1 条进入街道为绿灯，即 | | `rue-de-moscou 1` | `rue-de-moscou` 每周期绿灯 1 秒（对 `rue-de-moscou` 始终为绿灯）。 | #### 评分 每辆在模拟结束前完成其路径的车辆都会获得分数。对于在时间 $T$ 完成路径的车辆，奖励分数为 $F$ 分（完成路径的固定奖励），外加 $D - T$ 分。（车辆完成路径时每剩余一秒得一分。） 换句话说：如果一辆车在时间 $T$ 完成，则得分为 - 如果 $T \leq D$，则为 $F + (D - T)$ 分， - 否则为 0 分。 解决方案的分数是所有车辆的分数之和。 #### 示例 例如，在上面的示例中，第一辆车： - $T = 0$：立即通过交叉口 0，因为那里的交通信号灯始终是绿灯， - $T = 1$：一秒后，它已经通过了 **rue-d-amsterdam**。然而，信号灯是**红色的**（因为对于交叉口 1，提交已将 **rue-d-athenes** 的信号灯设置为绿灯持续 2 秒）， - $T = 2$：该车现在通过交叉口并继续前往 **rue-de-moscou**， - $T = 5$：该车到达 **rue-de-moscou** 的终点，发现交叉口 2 是**绿灯**，通过它并继续前往 **rue-de-rome**。 第一辆车本应在 $T = 7$ 时到达 **rue-de-rome** 的终点，但这超过了运行截止时间（在输入数据集中定义）。这意味着该车获得 **0 分**。 第二辆车： - $T = 0$：发现交叉口 1 是绿灯并继续前往 **rue-de-moscou**， - $T = 3$：到达 **rue-de-moscou** 的终点，发现交叉口 2 是绿灯且没有车辆等待，因此立即通过交叉口并前往 **rue-de-londres**， - $T = 4$：该车到达 **rue-de-londres** 的终点，即其目的地。 因此第二辆车在截止时间前完成，并获得 $1000 + (6 - 4) = 1002$ 分。 此提交的最终分数为 **1002**。 **注意，有多个数据集代表问题的单独实例。你团队的最终得分将是各个数据集最佳得分的总和。** 你需要在本题中获得总共不低于 9700000 分，才可以被视作通过本题。赛场上的最高分是 10586135 分。 翻译由 DeepSeek 完成