P15277 [MCO 2025] Rectangle Connections

MCO 大陆可以看作是一个无限的二维网格。网格的行从下到上编号为 $0,1,2,\ldots$，列从左到右编号为 $0,1,2,\ldots$。位于第 $x$ 列、第 $y$ 行的单元格称为单元格 $(x,y)$。 MCO 大陆共有 $m$ 个区域。每个区域可以建模为 MCO 大陆上的一个矩形子网格。第 $i$ 个区域由四个整数 $(x_{i,1},x_{i,2},y_{i,1},y_{i,2})$ 表示，其中 $x_{i,1}\le x_{i,2}$ 且 $y_{i,1}\le y_{i,2}$。这意味着该区域包含所有满足 $x_{i,1}\le x\le x_{i,2}$ 且 $y_{i,1}\le y\le y_{i,2}$ 的单元格 $(x,y)$。 MCO 大陆的领导者 Evirir 希望建造邮局和道路，以服务 MCO 大陆的所有区域。 初始时，没有任何道路。首先，Evirir 可以任意连接多个区域，修建水平或垂直的道路（免费）。形式化地，两个区域 $i$ 和 $j$ **可以**通过道路连接，**当且仅当**： - 区间 $[x_{i,1},x_{i,2}]$ 与 $[x_{j,1},x_{j,2}]$ 相交（可能在边界处），**或** - 区间 $[y_{i,1},y_{i,2}]$ 与 $[y_{j,1},y_{j,2}]$ 相交（可能在边界处）。 特别地，如果两个区域的矩形有重叠，则它们可以通过道路连接。 在此之后，Evirir 可以选择任意数量的区域，并在其中每个区域建造一个邮局。最终，所有区域都必须（直接或间接）连接到至少一个邮局。一个区域连接到某个邮局，当且仅当该区域本身包含一个邮局，或者可以通过道路从该区域到达一个包含邮局的区域。 道路可以相互交叉，也可以穿过某个区域。但是，如果一条道路与另一条道路交叉，则不能在交叉点切换道路（这些道路是立交桥）。 Evirir 至少需要建造多少个邮局？

第一行包含一个整数 $m$ （$1\le m\le2\cdot{10}^5$），表示 MCO 大陆中区域的数量。 接下来 $m$ 行中的第 $i$ 行包含四个以空格分隔的整数 $x_{i,1}$， $x_{i,2}$， $y_{i,1}$ 和 $y_{i,2}$ （$0\le x_{i,1}\le x_{i,2}\le10^9$， $0\le y_{i,1}\le y_{i,2}\le10^9$），代表第 $i$ 个区域 $(x_{i,1},x_{i,2},y_{i,1},y_{i,2})$。

输出一个整数，表示需要建造的最少邮局数量。

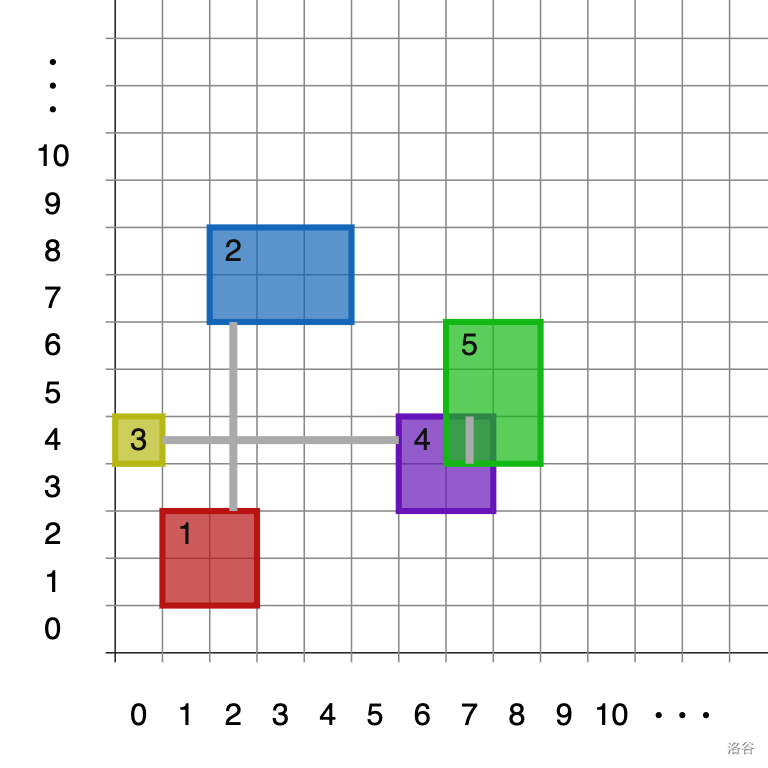
#### 注释 :::align{center}  ::: 在示例测试用例中，有三条道路，分别连接区域 1 与 2、区域 3 与 4、区域 4 与 5。**Evirir** 可以在区域 1 和区域 4 建造两个邮局。这样，区域 1 和区域 2 连接到区域 1 的邮局，区域 3、4 和 5 连接到区域 4 的邮局。可以证明，仅建造 1 个邮局是不够的。 请注意，尽管道路在单元格 $(2,4)$ 处交叉，但不能在交叉点切换道路。例如，区域 1 和区域 3 并不连通。 #### 计分 **子任务 1** （$4$ 分）： 存在某个常数 $c$，使得对于所有 $1\le i\le m$，有 $y_{i,1}=y_{i,2}=c$。 **子任务 2** （$16$ 分）： $m\le2000$，且对于所有 $1\le i\le m$，有 $0\le x_{i,1},x_{i,2},y_{i,1},y_{i,2}\le2000$。 **子任务 3** （$9$ 分）： $m\le2000$。 **子任务 4** （$12$ 分）： 对于所有 $1\le i\le m$，有 $x_{i,1}=x_{i,2}$ 且 $y_{i,1}=y_{i,2}$。 **子任务 5** （$32$ 分）： 对于所有 $1\le i\le m$，有 $y_{i,1}=y_{i,2}=i$。 **子任务 6** （$14$ 分）： 对于所有 $1\le i\le m-1$，有 $x_{i,1}\le x_{(i+1),1}$ 且 $y_{i,1}\le y_{(i+1),1}$。 **子任务 7** （$13$ 分）： 无额外限制。 翻译由 DeepSeek 完成