P15277 [MCO 2025] Rectangle Connections

MCO Land can be modelled as an infinite 2D grid. The rows of the grid are numbered $0,1,2,\ldots$ from bottom to top, and the columns are numbered $0,1,2,\ldots$ from left to right. The cell on column $x$ and row $y$ is called cell $(x,y)$. MCO land consists of $m$ districts. Each district can be modelled as a rectangular subgrid in MCO land. The $i$-th district is represented by four integers $(x_{i,1},x_{i,2},y_{i,1},y_{i,2})$ where $x_{i,1}\le x_{i,2}$ and $y_{i,1}\le y_{i,2}$. This means that the district consists of cells $(x, y)$ such that $x_{i,1}\le x\le x_{i,2}$ and $y_{i,1}\le y\le y_{i,2}$. Evirir, the leader of MCO Land, wants to build post offices and roads to service all districts of MCO Land. Initially, there are no roads. Firstly, Evirir can connect as many districts as desired with horizontal or vertical roads (for free). Formally, two districts $i$ and $j$ can be connected by a road if and only if: - the intervals $[x_{i,1},x_{i,2}]$ and $[x_{j,1},x_{j,2}]$ intersect (possibly at the boundary), OR - the intervals $[y_{i,1},y_{i,2}]$ and $[y_{j,1},y_{j,2}]$ intersect (possibly at the boundary). Notably, if two districts' rectangles overlap, then they can be connected by a road. After that, Evirir can choose any number of districts and build a post office in each of them. In the end, all districts must be (directly or indirectly) connected to at least one post office. A district is connected to a post office if it contains a post office, or it is possible to travel from it to a district that contains a post office using roads. Roads may cross over another road or district. However, if a road crosses another road, one cannot switch roads at the crossing point (the roads are overpasses). What is the minimum number of post offices that Evirir needs to build?

The first line contains an integer $m$ ($1\le m\le2\cdot{10}^5$), the number of districts in MCO Land. The $i$-th of the next $m$ lines will contain four space-separated integers, $x_{i,1}$, $x_{i,2}$, $y_{i,1}$, and $y_{i,2}$ ($0\le x_{i,1}\le x_{i,2}\le10^9$, $0\le y_{i,1}\le y_{i,2}\le10^9$), representing the $i$-th district $(x_{i,1},x_{i,2},y_{i,1},y_{i,2})$.

Output a single integer, the minimum number of post offices that need to be built.

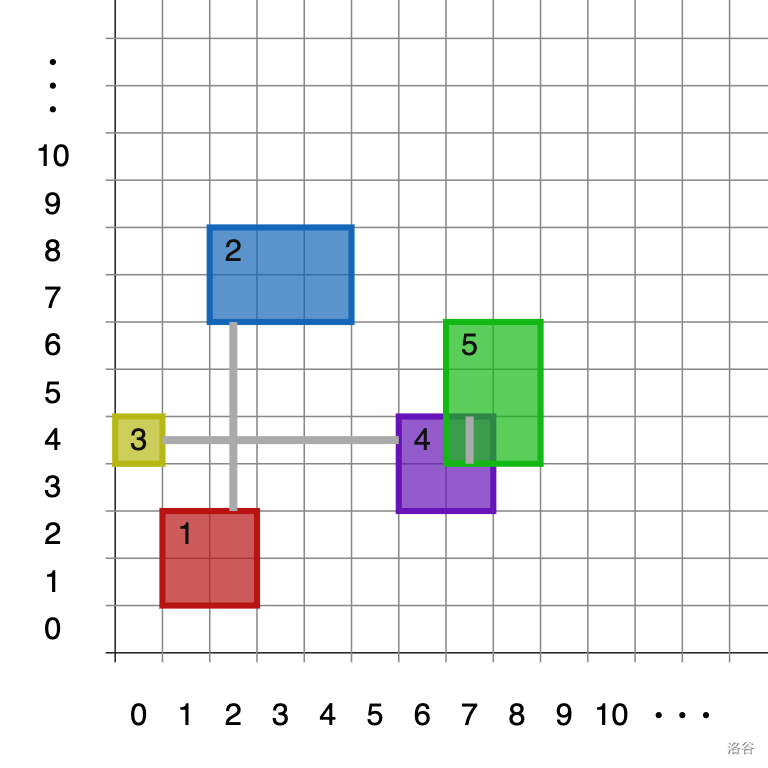
### Note :::align{center}  ::: In the example test case, there are three roads connecting districts 1 and 2, 3 and 4, and 4 and 5, respectively. Evirir can build two post offices at district 1 and 4. Then, districts 1 and 2 are connected to district 1's post office, and districts 3, 4, and 5 are connected to district 4's post office. It can be proven that 1 post office is not enough. Note that even though the roads cross at cell $(2,4)$, you cannot switch between roads. For example, districts 1 and 3 are not connected. ### Scoring Subtask 1 ($4$ points): For some constant $c$, $y_{i,1}=y_{i,2}=c$ for all $1\le i\le m$. Subtask 2 ($16$ points): $m\le2000$. $0\le x_{i,1},x_{i,2},y_{i,1},y_{i,2}\le2000$ for all $1\le i\le m$. Subtask 3 ($9$ points): $m\le2000$. Subtask 4 ($12$ points): $x_{i,1}=x_{i,2}$, $y_{i,1}=y_{i,2}$ for all $1\le i\le m$. Subtask 5 ($32$ points): $y_{i,1}=y_{i,2}=i$ for all $1\le i\le m$. Subtask 6 ($14$ points): $x_{i,1}\le x_{(i+1),1}$, $y_{i,1}\le y_{(i+1),1}$ for all $1\le i\le m-1$. Subtask 7 ($13$ points): No additional constraints.