P15310 [VKOSHP 2025] New Balls

This is an interactive problem. Usually, participants of the VKOSHP receive balls for each solved problem, but this time, for each solved problem, the team will be given a tree! Recall that a tree is a connected undirected graph without cycles. Since there are $n$ problems in the contest, it is necessary to prepare $n$ different trees, each containing $2n$ vertices, numbered from $1$ to $2n$. However, it turned out that trees tend to change constantly. If you start with some tree, before it is delivered to the team for the solved problem, the following operation can be applied to the tree no more than $n - 1$ times: - Choose numbers $a$, $b$, $c$, $d$ such that the edge $(a, b)$ is in the tree, and the edges $(c, d)$ are not in the tree; - Then, remove the edge $(a, b)$ from the tree and add the edge $(c, d)$. It is guaranteed that after this operation, the graph will remain a tree. You are interested in distinguishing the solved problems of each team, so you need to find $n$ trees such that they can be distinguished from each other even after the described modifications. 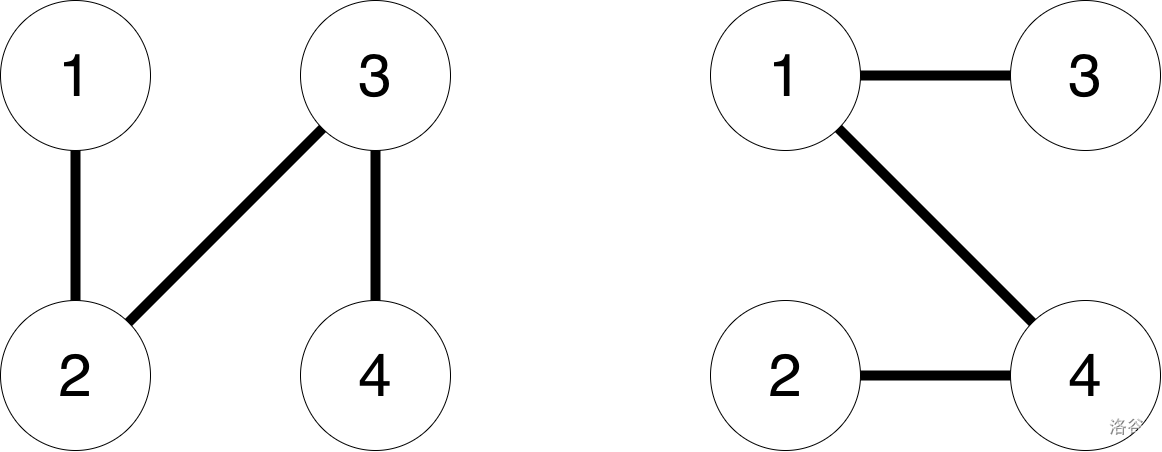:::align{center}  ::: The image above shows an example of balls from test cases for $n = 2$. 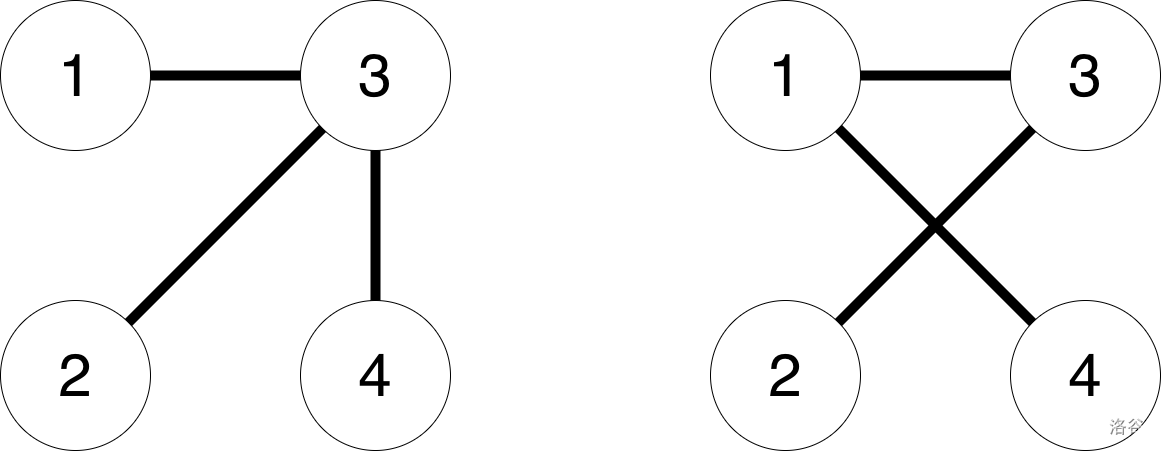:::align{center}  ::: The trees above show an example of the required trees from the test cases for your program. The testing of this problem is organized as follows. First, you report to the jury program $n$ trees, each containing $2n$ vertices. After that, you will be given $q$ trees in turn, each of which was obtained from one of your trees by applying no more than $n-1$ of the operations described above. For each tree, you must indicate which original tree it was derived from. ### Interaction Protocol First, your program should read from standard input the numbers $n$ and $q$ ($1 \le n, q \le 100$). Then, it should output $n$ trees, for each tree you need to output $2n - 1$ pairs of numbers---description of the edges of the tree. After that, the jury program will give you $q$ times a tree obtained from operations described above, and for each query, you must output a single number $x$---the index of the original tree from which the jury's tree was obtained.

N/A

N/A

In sample test interaction messages between the jury program and the contestant program are separated by empty lines to visualize which message is a response to which. In real interaction there will be no emptly lines and you should not print any. ### Note After each action of your program, output a newline. After each action of your program, flush the output stream.