P15310 [VKOSHP 2025] New Balls

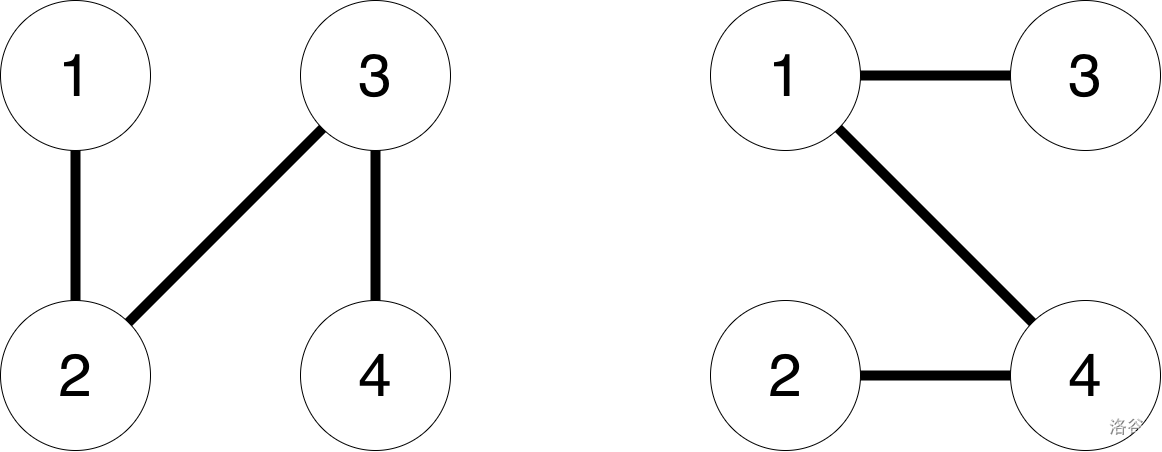
这是一个交互题。 通常，VKOSHP 的参赛者每解决一个问题就会获得一个球，但这一次，每解决一个问题，队伍将获得一棵树！回忆一下，树是一个没有环的连通无向图。 由于比赛中共有 $n$ 个问题，需要准备 $n$ 棵不同的树，每棵树包含 $2n$ 个顶点，编号从 $1$ 到 $2n$。 然而，事实证明树木会不断变化。如果你从某棵树开始，在它被交给解决该问题的队伍之前，可以对这棵树进行不超过 $n - 1$ 次以下操作： - 选择数字 $a$、$b$、$c$、$d$，使得边 $(a, b)$ 在树中，而边 $(c, d)$ 不在树中； - 然后，从树中移除边 $(a, b)$ 并添加边 $(c, d)$。保证在此操作后，图仍然是一棵树。 你希望对每个队伍解决的问题进行区分，因此你需要找到 $n$ 棵树，使得即使经过上述修改，它们也能被相互区分。 :::align{center}  ::: 上图展示了当 $n = 2$ 时测试用例中的“球”的示例。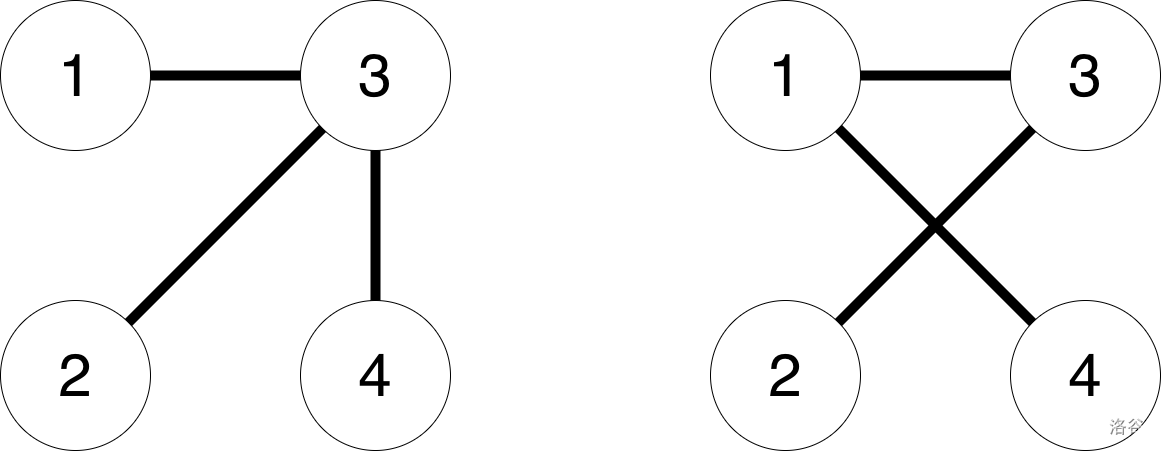 :::align{center}  ::: 上面的树展示了你的程序在测试用例中所需输出的树的示例。 这个问题的测试按如下方式组织。首先，你向评测程序提交 $n$ 棵树，每棵树包含 $2n$ 个顶点。 之后，你将会依次收到 $q$ 棵树，每棵树都是通过对你的某棵树应用不超过 $n-1$ 次上述操作得到的。对于每棵树，你必须指明它是由哪一棵原始树派生出来的。 ### 交互协议 首先，你的程序应从标准输入读取两个数字 $n$ 和 $q$（$1 \le n, q \le 100$）。 然后，它应输出 $n$ 棵树，对于每棵树，你需要输出 $2n - 1$ 对数字——该树边的描述。 之后，评测程序将 $q$ 次给你一棵由上述操作得到的树，对于每次查询，你必须输出一个数字 $x$——评测程序给出的这棵树是由哪一棵原始树（的索引）得到的。

无

无

在样例交互中，评测程序和参赛者程序之间的消息用空行分隔，以便直观显示哪个消息是对哪个消息的响应。在实际交互中，不会有空行，你也不应打印任何空行。 #### 注释 在你的程序每次输出后，输出一个换行符。 在你的程序每次输出后，刷新输出流。 翻译由 DeepSeek 完成