P15314 [VKOSHP 2025] Beaver Dam

这是一个交互题。 海狸水坝是一个由 $n \times m$ 个单元格组成的矩形，某些相邻单元格之间有秘密通道，海狸可以利用这些通道移动。水坝有 $k$ 个出口——即矩形中那些可以游出水坝的单元格。 科学家们试图弄清楚海狸水坝的结构。他们已经确定了其布局——确切地知道哪些相邻单元格之间有通道。同时已知，通道图构成了一棵树——这意味着任意两个单元格之间通过通道存在唯一路径，且每个单元格在路径中最多经过一次。不幸的是，科学家们目前对出口知之甚少——他们只知道 $k \geq 1$，即至少有一个出口。 为了找到水坝的出口，科学家们决定使用实验海狸。海狸是聪明的动物，它们完全了解自己水坝的布局，包括所有出口的位置。由于科学家们只剩下少数海狸可用于实验，他们最多只能进行 $48$ 次实验。 实验过程如下。科学家取出两只海狸，将它们分别释放到矩形水坝的单元格 $(i_1, j_1)$ 和 $(i_2, j_2)$ 中。之后，每只海狸将通过通道游向最近的出口。一切发生得非常快，因此科学家们只能确定哪只海狸先到达出口。如果两只海狸同时到达出口，则实验结果不确定——即可能是第一只先到，也可能是第二只先到。 科学家们需要从内部研究海狸水坝，因此他们需要发现至少一个水坝的出口。请帮助他们找到它。 ### 交互协议 开始时，你的程序需要读取测试参数。 第一行包含两个整数 $n$、$m$——水坝的尺寸（$2 \leq n, m \leq 10^6$； $4 \leq n \cdot m \leq 10^6$）。 接下来的 $n$ 行包含字符串 $h_i$，长度为 $m - 1$，由 $0$ 和 $1$ 组成，描述水坝中的水平通道：如果 $h_{i,j}=1$，则在单元格 $(i, j)$ 和 $(i, j+1)$ 之间存在直接通道。 接下来的 $n-1$ 行包含字符串 $v_i$，长度为 $m$，由 $0$ 和 $1$ 组成，描述水坝中的垂直通道：如果 $v_{i,j}=1$，则在单元格 $(i, j)$ 和 $(i+1, j)$ 之间存在直接通道。 然后，你的程序开始与评测程序交互，进行查询并接收实验结果。你可以执行题目描述中所述的操作，最多不超过 $48$ 次。 要提出询问，请输出格式为

无

无

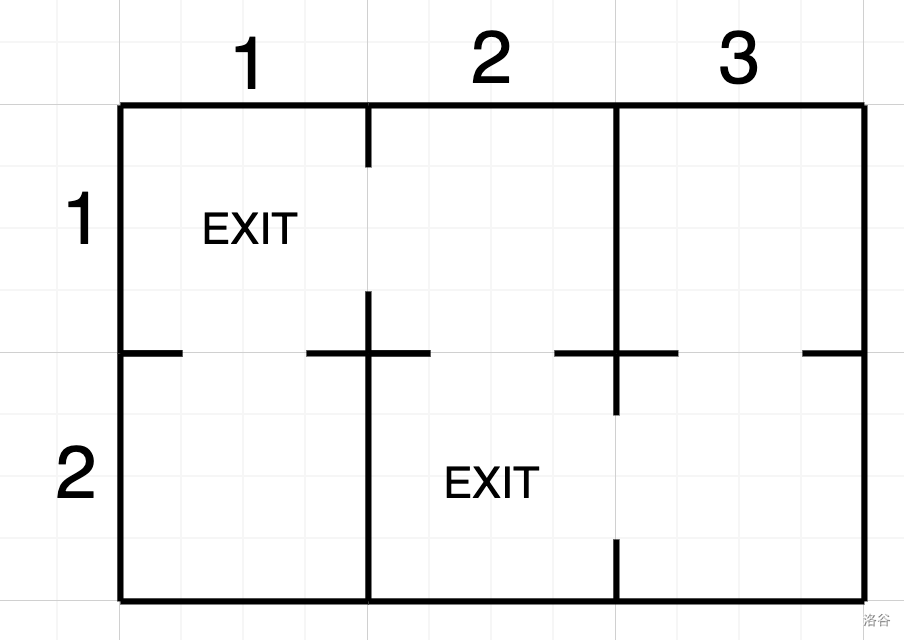
在样例交互中，评测程序和参赛者程序之间的消息用空行分隔，以便直观显示哪个消息是对哪个消息的响应。在实际交互中，不会有空行，你也不应打印任何空行。 在题目描述的示例中，迷宫如图所示： :::align{center}  ::: 即，水坝的出口位于点 $(1, 1)$ 和 $(2, 2)$。 翻译由 DeepSeek 完成