P15314 [VKOSHP 2025] Beaver Dam

This is an interactive problem. The beaver dam is a rectangle consisting of $n \times m$ cells, with secret passages between some neighboring cells that beavers can use to move. The dam has $k$ exits --- cells in the rectangle from which one can swim out of the dam. Scientists are trying to understand the structure of the beaver dam. They have already determined its layout --- it is known exactly which neighboring cells have passages. It is also known that the graph of passages forms a tree --- meaning there is a unique path through the passages between any two cells, visiting each cell no more than once. Unfortunately, the scientists have not yet been able to learn much about the exits --- they only know that $k \geq 1$, meaning there is at least one exit from the dam. To find an exit from the dam, the scientists decided to use test beavers. Beavers are intelligent animals, and they know the layout of their dam perfectly, including the location of all exits. Since the scientists have only a few beavers left for testing, they can conduct the experiment no more than $48$ times. The experiment works as follows. The scientists take two beavers and release them in the cells $(i_1, j_1)$ and $(i_2, j_2)$ of the rectangular dam. After that, each beaver will swim through the passages to the nearest exit. Everything happens incredibly quickly, so the scientists can only determine which beaver reached the exit faster. If both beavers reach the exit at the same time, the result of the experiment is undefined --- meaning either the first beaver or the second could arrive first. The scientists need to study the beaver dam from the inside, so they need to discover at least one exit from the dam. Help them find it. ### Interaction Protocol At the beginning, your program reads the test parameters. The first line contains two integers $n$, $m$---the dimensions of the dam ($2 \leq n, m \leq 10^6$; $4 \leq n \cdot m \leq 10^6$). The next $n$ lines contain strings $h_i$ of length $m - 1$ consisting of $0$s and $1$s, describing the passages in the dam: if $h_{i,j}=1$, then there is a direct passage between the cells $(i, j)$ and $(i, j+1)$. The next $n-1$ lines contain strings $v_i$ of length $m$ consisting of $0$s and $1$s, describing the vertical passages in the dam: if $v_{i,j}=1$, then there is a direct passage between the cells $(i, j)$ and $(i+1, j)$. Then your program interacts with the jury's program, making queries and receiving the results of the experiments. You can perform the action described in the statement no more than $48$ times. To ask a question, output a string in the format , after which 2 beavers will be released into the dam at the specified points $(i_1, j_1)$ and $(i_2, j_2)$. The conditions $1 \leq i_1, i_2 \leq n$; $1 \leq j_1, j_2 \leq m$ must be satisfied. In response, the jury's program outputs: - $1$, if the first beaver reaches the exit no later than the second; - $2$, if the second beaver reaches the exit no later than the first; - Any of the two verdicts above if the beavers reach the exits simultaneously. To output the answer to the problem, output the string $\tt{!\ i\ j}$, where $i$ and $j$ should be the row and column numbers where one of the exits is located. This output does not count towards the number of queries. If there are multiple exits in the dam, you can output any of them. After that, the interactor will output a verdict--- $\texttt{Win}$, if your guess is correct, and $\texttt{Lose}$ otherwise. If your answer was incorrect, your solution will receive a verdict of $\texttt{WA}$ (Wrong Answer) and terminate. To avoid receiving incorrect verdicts, your solution should also terminate if it receives information that the outputted answer was incorrect. If at any point your program exceeds the limit of $48$ queries, your program will terminate with a verdict of $\texttt{WA}$. After each action of your program, output a newline. After each action of your program, flush the output stream. Note that in this problem, the interactor may be adaptive, meaning the state of the maze always corresponds to the queries already made, but otherwise may change during the execution.

N/A

N/A

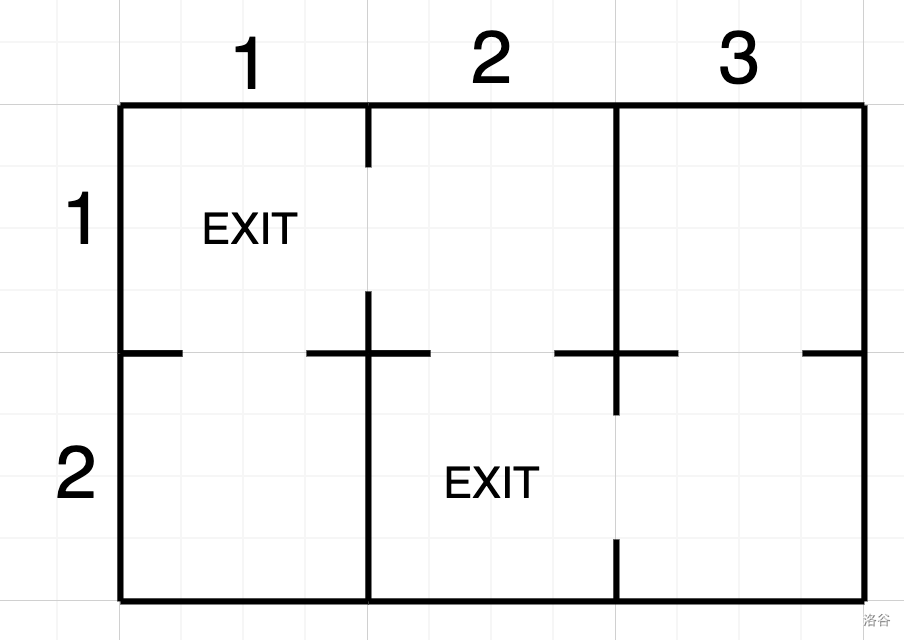
In sample test interaction messages between the jury program and the contestant program are separated by empty lines to visualize which message is a response to which. In real interaction there will be no emptly lines and you should not print any. In the example from the statement, the maze looks like this: :::align{center}  ::: That is, the exits in the dam are located at points $(1, 1)$ and $(2, 2)$.