P15328 [GCPC 2025] Around the Table

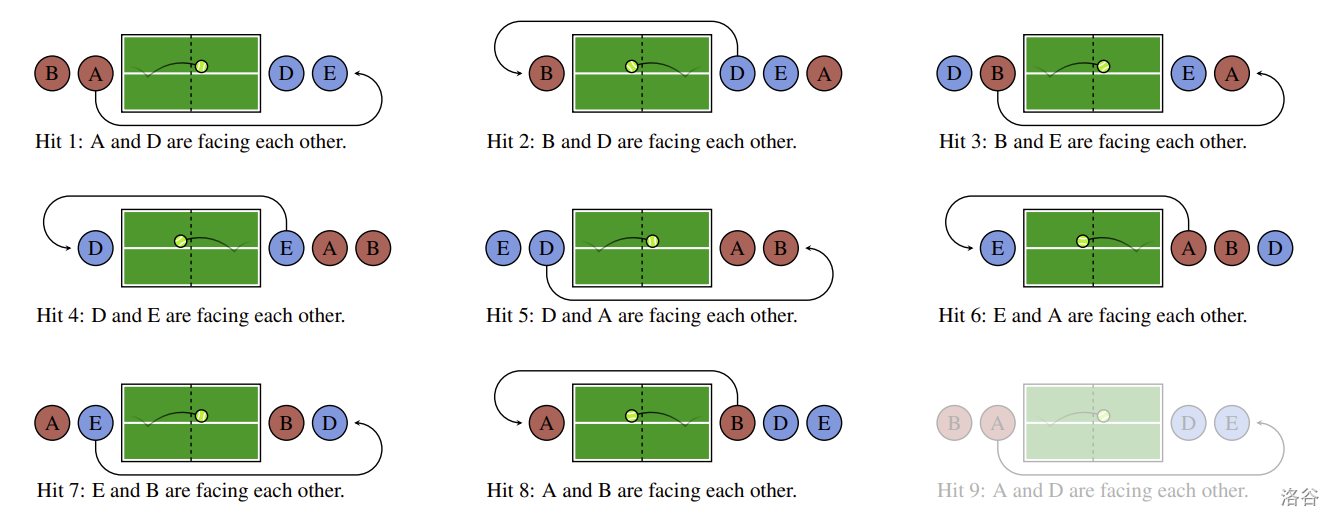
艾米莉亚和她的兄弟亚历克斯与许多朋友在公园里相遇，一起打乒乓球。由于只有一张球桌，他们玩起了大家最喜欢的“轮转球”游戏。 规则很简单：球桌左侧有 $\ell \geq 2$ 个孩子排队，右侧有 $r \geq 1$ 个孩子排队。左侧的第一个孩子开始发球。持球者将球击过网到对面，然后跑到对面队伍的末尾排队。如此重复，直到第一次失误。 :::align{center}  图 A.1：第一个样例的可视化。在第 1 次和第 5 次击球，以及第 3 次和第 7 次击球时，我们观察到相同的配对。经过 8 次击球后，我们回到了初始状态，之后无法观察到任何新的配对。因此，总共会看到 6 种不同的配对。 ::: 艾米莉亚、亚历克斯和他们的朋友们经常玩这个游戏，并且技术非常好，几乎可以永远打下去而不犯任何错误。过了一段时间，艾米莉亚注意到她从未与亚历克斯对阵过，也就是说他们从未同时站在对面队列的最前面。她想知道在这一轮游戏中是否会发生这种情况。出于好奇，她开始记录哪些配对已经互相交过手。 经过 $10^{10^{100}}$ 次击球后，她一共会记录到多少种不同的配对？

输入包含： - 一行两个整数 $\ell$ 和 $r$（$2 \leq \ell \leq 10^9$，$1 \leq r \leq 10^9$），分别表示球桌左侧和右侧的玩家人数。

输出一个整数，表示艾米莉亚记录到的不同配对的数量。

翻译由 DeepSeek 完成