P15330 [GCPC 2025] Congklak

爱丽丝和比尔非常喜欢玩桌游，并且总是在寻找新的挑战。最近，他们发现了一种印度尼西亚游戏 **Congklak**，这个游戏在一个由若干洞组成的游戏板上进行，每个洞里有一些石子。玩了几局后，爱丽丝很快掌握了要领并且赢了每一局，所以比尔不想再玩了。取而代之，受到游戏规则的启发，他给爱丽丝提出了以下挑战： 有一个游戏板，上面有 $n$ 个洞排成一长排。这些洞从左到右编号为 1 到 $n$。初始时，第 $i$ 个洞中有 $a_i$ 颗石子。注意，这个设置不同于通常的 Congklak 游戏，通常的游戏板由两排洞组成，两端各有一个大洞。 现在比尔将进行 $t$ 局游戏，每局游戏过程如下： 比尔从第一个洞开始，手里拿着一颗新的石子。然后他沿着游戏板从洞 1 移动到洞 $n$。在每个洞 $i$ 处，他首先检查当前洞中有多少颗石子，并根据结果执行以下两个操作之一： 1. 如果洞是空的，他将一颗石子放入其中。然后他检查手里还剩多少颗石子。如果手里空了，游戏停止。否则，他将手移动到下一个洞 $i+1$ 并重复这些步骤。 2. 如果洞里至少有一颗石子，他也将一颗石子放入其中。然后他检查手里还剩多少颗石子。如果手里空了，他将从洞 $i$ 中取出所有石子到手里。无论手里是否空了，他都会将手移动到下一个洞 $i+1$ 并重复这些步骤。 当比尔的手移动经过洞 $n$ 时，游戏停止，比尔丢弃手里剩余的任何石子。 比尔向爱丽丝发起挑战，要求她预先预测在恰好进行 $t$ 局游戏之后每个洞中的石子数。注意，游戏板在每局游戏结束后**不会**重置，即第二局游戏的初始配置与第一局游戏结束时的配置相同。

输入包含： - 一行两个整数 $n$ 和 $t$（$1 \leq n \leq 10^5$，$1 \leq t \leq 10^{12}$），分别表示洞的数量和游戏局数。 - 一行 $n$ 个整数 $a_1, \dots, a_n$（$0 \leq a_i \leq 10^{12}$），其中 $a_i$ 描述第 $i$ 个洞中初始的石子数。

输出 $n$ 个整数，第 $i$ 个整数表示进行 $t$ 局游戏后第 $i$ 个洞中的石子数。

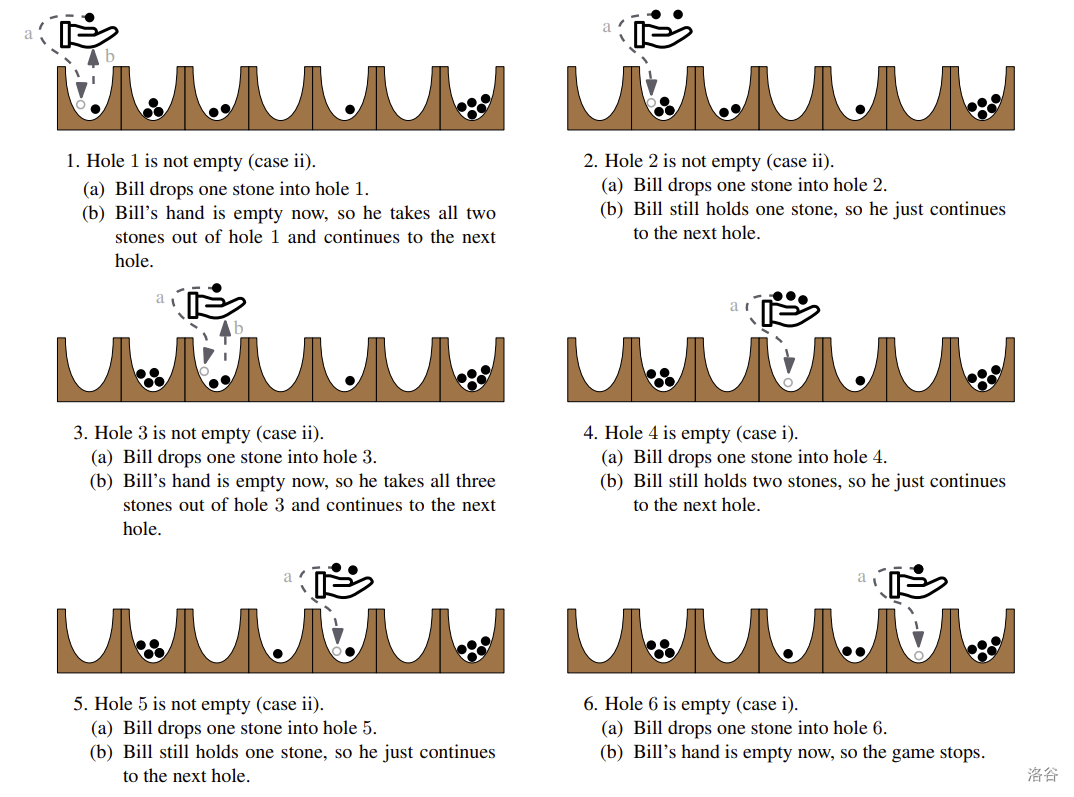
#### 样例 1 解释 在第一个样例中，比尔只玩了一局游戏。下图展示了这局游戏中执行的步骤。 :::align{center}  ::: #### 样例 2 解释 在第二个样例中，每个洞的初始石子数为 $[1000000000000, 1, 2, 3]$。每局游戏后每个洞的石子数为： 1. $[0, 2, 3, 4]$ 2. $[1, 2, 3, 4]$ 3. $[0, 3, 0, 5]$ 4. $[1, 3, 0, 5]$ 翻译由 DeepSeek 完成