P15331 [GCPC 2025] Demand for Cycling

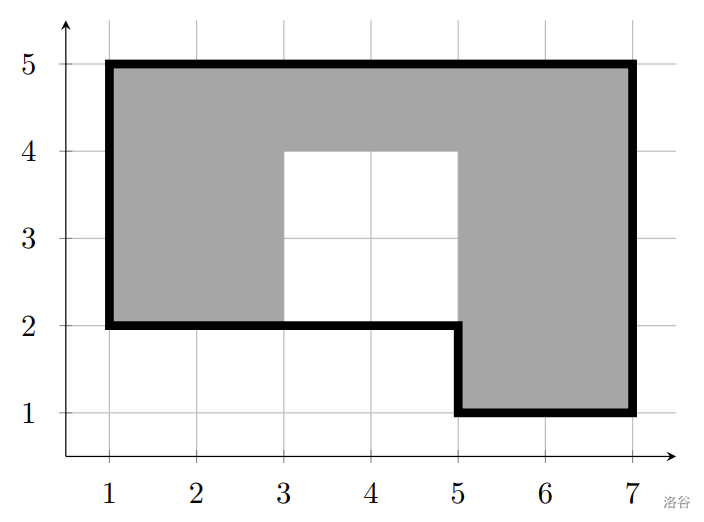
在垂直骑行网格城（简称 GCPC）中，汽车从未流行过。相反，每个人都使用各种类型的自行车在城市中穿行。这并不是 GCPC 的唯一特色。遵循一种至少自公元前 2600 年起就在不同地方使用的古老城市设计，所有街道都沿着基本方向（即正北/正南或正东/正西）延伸，因此只以直角相交。 市议会计划新增一条环绕整个城市的自行车道，以满足对良好骑行基础设施的强烈需求。这条新自行车道应当尊重古老的网格系统，因此只能由平行于基本方向的线段组成。 为了最小化建设成本以及骑行者的通行时间，市议会希望这条新自行车道尽可能短。议会已经准备好了城市的轮廓，但现在需要帮助来找到这样一条最短的自行车道。为简化起见，你可以假设自行车道的宽度为零，并且可以与城市轮廓上的任意点距离为零。 :::align{center}  图 D.1：第一个样例的图示。灰色区域代表城市，黑色轮廓是一条最优的自行车道。给出的自行车道长度为 20。可以证明不存在更短的满足要求的路径。 :::

输入包含： - 一行一个整数 $n$（$4 \leq n \leq 10^5$），表示城市轮廓点的数量。 - 接下来 $n$ 行，每行两个整数 $x$ 和 $y$（$1 \leq x, y \leq 10^9$），表示点的坐标。 此外，保证： - 城市轮廓的点按逆时针顺序给出。 - 相邻两个点的横坐标相同或纵坐标相同。 - 没有连续三个点共线。 - 城市轮廓不自交。

输出一个整数 $m$（$m \leq n$），表示自行车道上的点数，随后 $m$ 行按逆时针顺序给出自行车道的坐标。注意，相邻两个点的横坐标必须相同或纵坐标相同，且不能有连续三个点共线。 如果有多个有效解，你可以输出任意一个。

翻译由 DeepSeek 完成