P15333 [GCPC 2025] Fair and Square

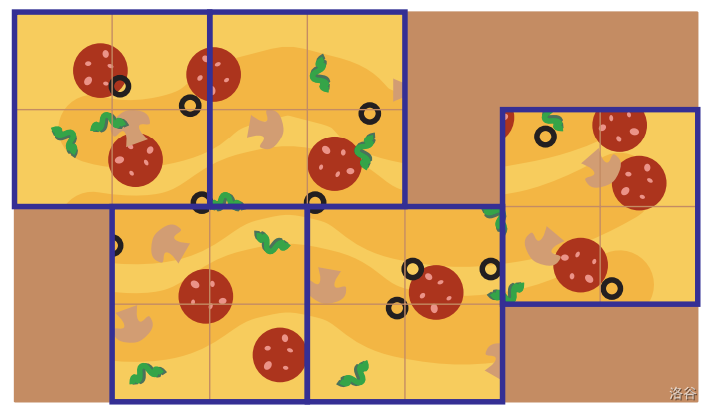
菲利克斯为自己的生日派对订购了一个巨大的矩形披萨。他只是快速地去厨房拿了些盘子和餐具，当他回来时，客人们已经开始自行取用披萨的不同部分了。这块原本由 $h \times w$ 个相同大小的正方形小块组成的披萨，现在缺失了其中一些小块： :::align{center}  图 F.1：第一个样例的图示，被分割成边长为 2 的正方形。 ::: 为了确保剩余披萨的分配进行得更有秩序，菲利克斯想把剩下的披萨划分成更大的正方形区域。菲利克斯只能沿着网格线切割，并且不能重新排列披萨的任何部分。每个正方形的边长必须相同，并且为了最小化所需的盘子数量，这个边长应尽可能大。 找出这个最大可能的边长。注意，答案总是存在，因为披萨总是可以被分成 $1 \times 1$ 的正方形。

输入包含： - 一行两个整数 $h$ 和 $w$（$1 \leq h, w \leq 2500$），网格的高度和宽度。 - 接下来 $h$ 行，每行一个长度为 $w$ 的字符串，由 `#`（表示仍在的披萨小块）和 `.`（表示已被取走的披萨小块）组成。 保证输入中至少包含一个 `#`。

输出一个整数，使得剩余的披萨可以被划分成该边长的正方形，并且该边长是可能的最大值。

翻译由 DeepSeek 完成