P15336 [GCPC 2025] Island Urbanism

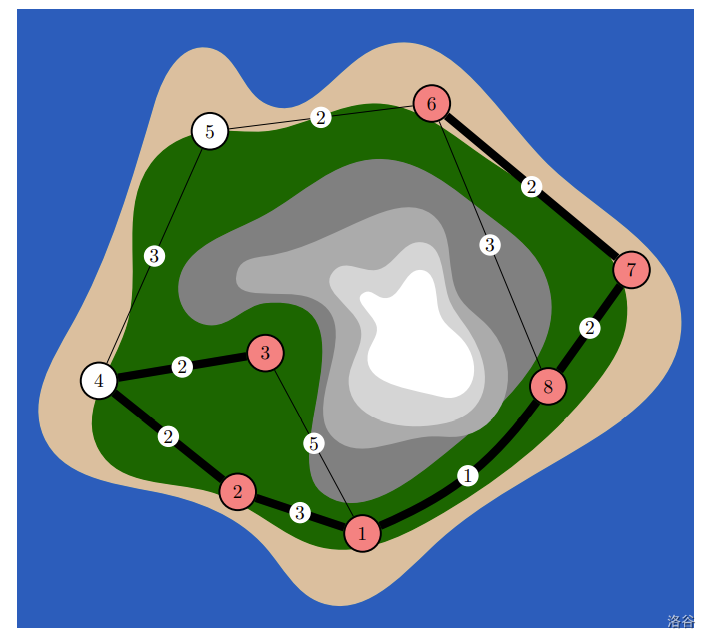
在一个远离任何大陆的小型火山岛上，**无痛骑行大议会（GCPC）** 经常收到关于自行车道网络质量差的投诉。他们的预算有限，但希望改善岛上所有骑行者的状况。一项调查帮助确定了骑行者最常去的目的地。GCPC 认为，如果能够仅使用新建的自行车道在任意两个目的地之间骑行，那么骑行者就会对自行车道的替换感到满意。为了不过分偏袒任何一个村庄，议会决定每个村庄最多应考虑 $7$ 个目的地。 :::align{center}  图 I.1：第二个样例的图示。村庄 1 由路口 1、2、3、4 组成，村庄 2 仅由路口 5 组成，村庄 3 由剩余路口组成。作为目的地的路口以红色标记。 ::: 有一条环绕火山的主要环形自行车道。沿途它恰好经过岛上的每个村庄一次。每个村庄可能还有额外的自行车道。为了通过新道路连接所有目的地，GCPC 至少需要花费多少来替换自行车道？

输入包含： - 一行四个整数 $n$、$m$、$v$ 和 $k$（$3 \leq n \leq 5000$，$n \leq m \leq 20\,000$，$3 \leq v \leq n$，$1 \leq k \leq n$），分别表示路口数量、自行车道数量、村庄数量和目的地数量。 - 一行 $v$ 个整数 $u_i$（$1 \leq u_i$，$\sum_{i=1}^{v} u_i = n$），其中第 $i$ 个数描述第 $i$ 个村庄中的路口数量。 - 接下来 $m$ 行，每行包含三个整数 $a$、$b$ 和 $c$（$1 \leq a, b \leq n$，$1 \leq c \leq 10^9$），描述一条连接路口 $a$ 和 $b$ 的双向自行车道，其替换成本为 $c$。 - 一行包含 $k$ 个互不相同的整数 $t$（$1 \leq t \leq n$），表示必须通过替换后的自行车道连接起来的路口。 此外，保证： - 村庄 1 由路口 $1, \dots, u_1$ 组成，村庄 2 由路口 $u_1 + 1, \dots, u_1 + u_2$ 组成，依此类推。最后一个村庄由路口 $1 + \sum_{i=1}^{v-1} u_i, \dots, n$ 组成。在每个村庄内部，可以在不离开村庄的情况下在任意一对路口之间通行。 - 对于每个 $1 \leq j \leq v - 1$，在路口 $\sum_{i=1}^{j} u_i$ 和 $1 + \sum_{i=1}^{j} u_i$ 之间存在一条自行车道，并且在路口 $n$ 和 $1$ 之间也存在一条自行车道。不同村庄之间没有其他自行车道。 - 每对路口之间至多有一条自行车道，且没有自行车道连接同一个路口。 - 在每个村庄中，需要成为改进骑行网络一部分的路口数量不超过 $7$ 个。

输出一个整数，表示允许替换自行车道的最小总成本，使得任意两个目的地之间的出行都只能使用新替换的道路完成。

翻译由 DeepSeek 完成