P15336 [GCPC 2025] Island Urbanism

On a small volcanic island far away from any major landmass, the **Grand Council for Painless Cycling (GCPC)** is facing regular complaints about the bad quality of the bike path network. Their budget is limited, but they would like to improve the situation for all the cyclists on their island. A survey helped to determine the most common destinations of the cyclists. The GCPC expects that the cyclists are satisfied with the bike path replacements if there is a way to cycle between any two destinations using only newly replaced bike paths. In order not to unduly favour any of the villages, the Council has decided that a maximum of $7$ destinations per village should be taken into account. 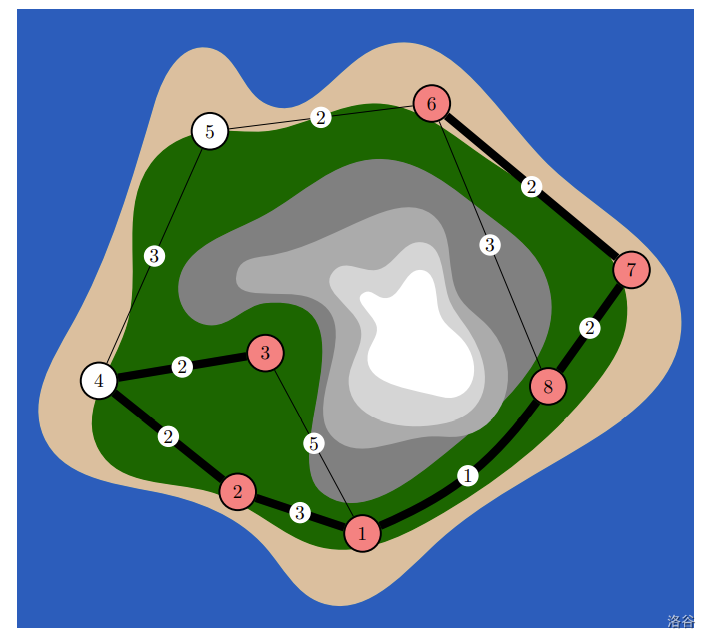:::align{center}  Figure I.1: Illustration of the second sample. Village 1 consists of Junctions 1, 2, 3, and 4, Village 2 consists only of junction 5, and Village 3 consists of the remaining junctions. Junctions that are destinations are coloured red. ::: There is one main cyclic bike path going around the volcano. On its way, it traverses every village on the island exactly once. Each village may have additional bike paths. How much does the **GCPC** have to spend at least in order to replace bike paths to connect all destinations via new paths?

The input consists of: - One line with four integers $n$, $m$, $v$ and $k$ ($3 \leq n \leq 5000$, $n \leq m \leq 20\,000$, $3 \leq v \leq n$, $1 \leq k \leq n$), the number of junctions, the number of bike paths, the number of villages, and the number of destinations. - One line with $v$ integers $u_i$ ($1 \leq u_i$, $\sum_{i=1}^{v} u_i = n$), the $i$th of which describes the number of junctions in village $i$. - $m$ lines each containing three integers $a$, $b$ and $c$ ($1 \leq a, b \leq n$, $1 \leq c \leq 10^9$), describing a bidirectional bike path between junction $a$ and junction $b$ with a replacement cost of $c$. - One line with $k$ distinct integers $t$ ($1 \leq t \leq n$), the junctions that have to be connected by the replaced bike paths. Additionally, the following is guaranteed: - Village 1 consists of junctions $1, \dots, u_1$, village 2 consists of junctions $u_1 + 1, \dots, u_1 + u_2$, and so on. The last village consists of junctions $1 + \sum_{i=1}^{v-1} u_i, \dots, n$. Within each village, it is possible to travel between any pair of junctions without leaving the village. - There is a bike path between junctions $\sum_{i=1}^{j} u_i$ and $1 + \sum_{i=1}^{j} u_i$ for each $1 \leq j \leq v - 1$, as well as a bike path between junctions $n$ and $1$. There are no other bike paths between different villages. - There is at most one bike path between each pair of junctions and no bike path connects a junction to itself. - In each village there are at most $7$ junctions that need to be part of the improved cycling network.

Output the minimum cost which allows replacing bike paths such that every trip between any two destinations can be done using only newly replaced paths.