P15346 [TOIP 2025] 煎餅攤

阿麥在假日市集裡擺了一個攤子賣煎餅。 考量每個人的食量不同，他決定販售 $n$ 種不同大小的煎餅，依照小到大由 $1$ 編號到 $n$，並預計將同一種大小的煎餅堆成一疊方便選購。 每疊煎餅至多只能疊 $m$ 片，否則會因為過高而倒塌。 阿麥每煎好一片就將該片煎餅放到攤位檯面上，但因為太過匆忙，不同大小的煎餅被堆放在同一疊。 當他注意到時，攤位上已有 $n$ 疊煎餅，每疊都恰有 $m$ 片，而每種大小的煎餅也恰有 $m$ 片。 阿麥想利用煎餅鏟來移動這些煎餅，調整回他預期的擺設。 他只能透過下面的動作來調整煎餅位置： - 將煎餅鏟插入某疊煎餅中的某兩片之間 - 將煎餅鏟上方所有的煎餅放置至另一疊的上方 （鏟子上方的煎餅順序不變） 因攤位檯面大小有限，除了既有的 $n$ 疊煎餅外，剩餘的空間僅能再容納一疊煎餅； 此外，調整過程不可有任一疊超過 $m$ 片，否則該疊煎餅就會倒塌。 請協助阿麥將同樣大小的煎餅調整為同一疊，並且讓較小的煎餅排在較左邊。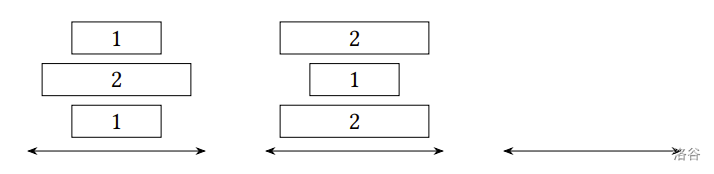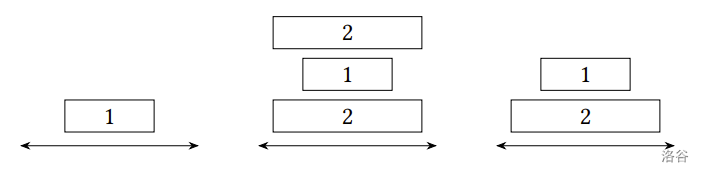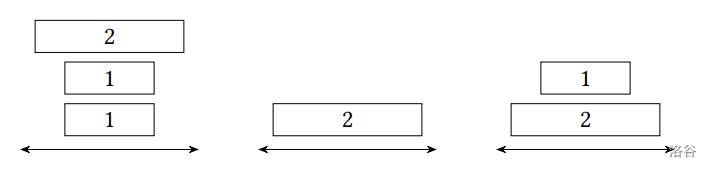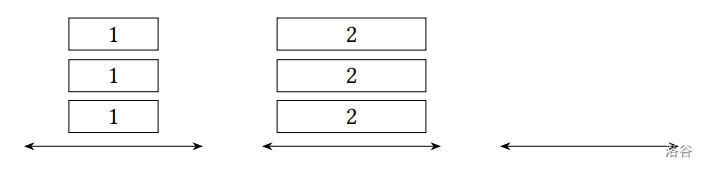 舉例來說，若 $n=2$，$m=3$，一開始的 $2$ 疊煎餅如下圖 （最右邊為檯面剩餘空間）： :::align{center}  ::: 一個可能的調整方式如下，將煎餅鏟插入最左邊的下面兩片之間，並移動至右方的剩餘空間： :::align{center}  ::: 將煎餅鏟插入中間的下面兩片之間，並移動至最左邊： :::align{center}  ::: 將最左邊最上面的煎餅鏟至中間： :::align{center}  ::: 接著再將最右邊的兩個煎餅分別鏟到第 $1$, $2$ 疊，便完成了阿麥預期的擺設方式： :::align{center}  ::: 請寫一個程式幫助阿麥將各種大小的煎餅移動到想要的位置， 由於移動方法很多可以輸出任何一種可行的移動方法， 但移動的次數需要在 $9nm$ 次以內。

$$ \begin{aligned} &m \; n \\ &a_{1,1} \; a_{1,2} \; \cdots \; a_{1,m} \\ &a_{2,1} \; a_{2,2} \; \cdots \; a_{2,m} \\ &\vdots \\ &a_{n,1} \; a_{n,2} \; \cdots \; a_{n,m} \end{aligned} $$ * $n$ 代表目前共有 $n$ 疊煎餅。 * $m$ 代表目前每疊煎餅恰有 $m$ 片煎餅，並且每種大小的煎餅都恰有 $m$ 片。 * $a_{i,j}$ 代表由左到右第 $i$ 疊，由下至上第 $j$ 個煎餅的大小。

$$ \begin{aligned} &c \\ &s_1 \; k_1 \; t_1 \\ &s_2 \; k_2 \; t_2 \\ &\vdots \\ &s_c \; k_c \; t_c \end{aligned} $$ * $c$ 代表移動的總次數。 * $s_i$, $k_i$, $t_i$ 代表第 $i$ 次的移動將從左到右第 $s_i$ 的上面 $k_i$ 片煎餅移動到從左到右的第 $t_i$ 疊。（第 $n+1$ 疊為開始時的空位） * $0 \le c \le 9nm$。 * $1 \le s_i, t_i \le n+1$，且 $s_i \neq t_i$。 * $k_i \ge 1$ 且不得大於當前第 $s_i$ 疊的煎餅數量。

### 測資限制 * $1 \le n \le 50$。 * $1 \le m \le 50$。 * $1 \le a_{i,j} \le n$。 * 所有輸入的數皆為整數。 * 保證 $1$ 到 $n$ 每個數字恰好在 $a$ 裡出現 $m$ 次。 ### 評分說明 本題共有三組子任務，條件限制如下所示。每一組可有一或多筆測試資料，該組分數為所有測試資料的最小得分。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | 8 | $m = 1$。 | | 2 | 37 | $n = 2$。 | | 3 | 55 | 無額外限制。 | 本題若輸出任意合法解答該測資以滿分計，但輸出若有下列非法情況測資則以 $0$ 分計： - 輸出的移動次數過多。 - 數字超出範圍。 - 移動的煎餅數量大於起始疊數的煎餅數量。 - 移動完畢後，第 $i$ 種煎餅沒有全部都在第 $i$ 疊的位置上。 另外，如果移動過程中有任一疊煎餅超過 $m$ 個，則該筆測資以原測資組分數 $30\%$ 計。