P15348 [TOIP 2025] 同色楼梯和双色楼梯

在一个 $m\times n$ 的方格图中，每一格都有恰一种颜色，我们用大写英文字母代表每种颜色。 所谓的「楼梯」是指：连续的某些直行的区段，这些区段的底部位置（下方所在的列）必须是一样的，而高度则是自左而右逐步加一。注意，一个楼梯图形的高度与宽度必然是相等的。 所谓的「同色楼梯」是指：一个楼梯其中所涵盖方格的颜色皆相同。 所谓的「双色楼梯」是指：一个楼梯其中所涵盖方格的颜色有恰两种。 按照以下的范例图形中，蓝色、黄色与绿色分别是宽度（高度）为 $2$、$3$ 与 $4$ 的「同色楼梯」。请注意，楼梯与楼梯可能重叠，例如蓝色 C 楼梯旁还有一个C楼梯。此外，大楼梯中必然有小楼梯，例如下图中宽度 $3$ 的 B 楼梯中有 $3$ 个宽度 $2$ 的楼梯。宽度 $4$ 的 A 楼梯中则含有 $3$ 个宽度 $3$ 的楼梯以及 $6$ 个宽度 $2$ 的楼梯。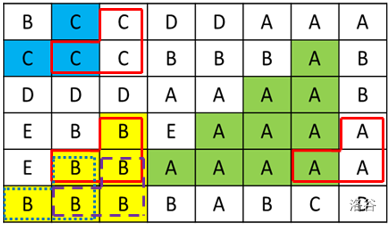 :::align{center}  ::: 以下的范例图形中，有标注出所有「双色楼梯」。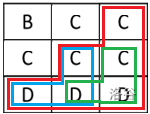 :::align{center}  ::: 你的任务是算出所有宽度（高度）的同色楼梯或双色楼梯分别有几个。

$$ \begin{aligned} &m \; n \\ &a_{1,1} a_{1,2} a_{1,3} \cdots a_{1,n} \\ &a_{2,1} a_{2,2} a_{2,3} \cdots a_{2,n} \\ &a_{3,1} a_{3,2} a_{3,3} \cdots a_{3,n} \\ &\vdots \\ &a_{m,1} a_{m,2} a_{m,3} \cdots a_{m,n} \\ &q \end{aligned} $$ * $m$、$n$ 分别代表区域高度、区域宽度。 * $a_{i,j}$ 代表该区域的颜色。 * 若 $q=1$ 代表询问同色楼梯数量。若 $q=2$ 代表询问双色楼梯数量。

$$ \begin{aligned} &k \\ &s_1 \; s_2 \; s_3 \; \cdots \; s_k \end{aligned} $$ * $k$ 为一非负整数，代表宽度（高度）最大的同色楼梯（双色楼梯）的宽度（高度）。 * $s_i$ 皆为非负整数，代表宽度（高度）为 $i$ 的同色楼梯（双色楼梯）数量。 * 若 $k = 0$，第二行输出一空行。

### 数据限制 * $1 \le m \le 4000$。 * $1 \le n \le 4000$。 * $a_{i,j}$ 为大写英文字母。 * $m$ 和 $n$ 皆为整数。 * $q \in \{1,2\}$。 ### 评分说明 本题共有五组子任务，条件限制如下所示。每一组可有一或多笔测试数据，该组所有测试数据皆需答对才会获得该组分数。 | 子任务 | 分数 | 额外输入限制 | | :------: | :----: | ------------ | | 1 | 5 | $q=1$，所有 $a_{i,j}$ 相同。 | | 2 | 9 | $q=1$，$m \le 200$, $n \le 200$。 | | 3 | 22 | $q=1$，$m \le 200$。 | | 4 | 33 | $q=1$。 | | 5 | 31 | $q=2$。 |