P15349 [TOIP 2025] 巡视农场
题目背景
本题测试数据极大(>4 GB),在洛谷评测中删除了 subtask 4 的最后两个测试点和 subtask6 的最后一个测试点。评测可能需要 2-4 分钟时间加载所有测试点。
由于读入测试数据需要大量时间(而在原比赛中似乎并不计入程序用时),本题时限相较原题时限翻倍。
本题测试数据根据比赛官方下发的数据生成器自行在本地生成,由于跨平台差异可能会和原题存在不同,但是使用的生成指令完全一致。
被删除的测试点可以在 评测。
题目描述
有一群人到了一个蛮荒之地开垦,经过很多努力,开辟了 $m$ 个农场,他们也开辟了一些道路连接这些农场,每一条道路连接两个不同的农场。由于道路开辟困难,总共只开辟了 $m-1$ 条道路,但任何两个农场之间,都有长度大于零的路径直接或间接连接。王老先生拥有其中的 $n$ 个农场,不过这些农场不一定全部直接连接在一起,可能有两个王老先生的农场之间,需要经过其他人的农场才能互相来回。
王老先生将他的农场由 $1$ 到 $n$ 编号,其中 $1$ 号农场也是他的住家。他记录了他的任两个农场之间的距离,想要规划出一条从住家($1$ 号农场)出发、巡视经过所有他的农场、最后回到住家的最短路径。当然,对于规划出的路径,各个农场经过的顺序与次数皆不限定,中间也可以经过其他人的农场。注意到王老先生并没有其他农场的信息,因此**王老先生只能通过这 $n$ 个农场两两之间的距离来计算最短路径**。
请你撰写一个程序,帮王老先生计算出最短的路径长度,满足该路径能巡视经过所有他的农场,最后回到住家。
举例来说,假设 $m=5$,而王老先生拥有其中的 $n=4$ 个农场。下图表示了所有 $m$ 个农场的结构,其中王老先生的农场被标上了 $1\sim 4$ 的编号:
:::align{center}
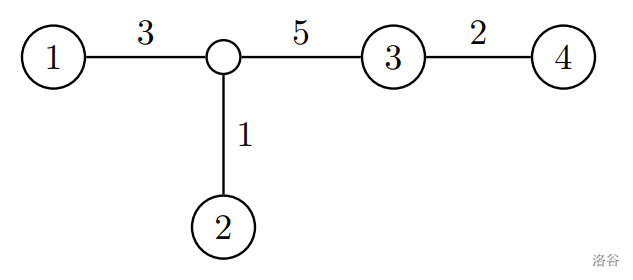
:::
由于王老先生记录了他的任两个农场之间的距离,我们可以将这些距离表示成如下的距离矩阵 $d$,其中 $d_{i, j}$(第 $i$ 列的第 $j$ 行)是农场 $i$ 到 $j$ 的距离。可以发现,一个距离矩阵必然是对称矩阵且对角线均为 $0$:
$$
\begin{array}{|c|c|c|c|}
\hline
0 & 4 & 8 & 10\\
\hline
4 & 0 & 6 & 8\\
\hline
8 & 6 & 0 & 2\\
\hline
10 & 8 & 2 & 0\\
\hline
\end{array}
$$
而通过距离矩阵提供給我们的信息,可以找出在这个例子中,最短的路径是 $1 \to 3 \to 4 \to 2 \to 1$,长度为 $8+2+8+4=22$。
输入格式
$$
\begin{aligned}
&n \\
&d_{1,1} \; d_{1,2} \; d_{1,3} \; \cdots \; d_{1,n} \\
&d_{2,1} \; d_{2,2} \; d_{2,3} \; \cdots \; d_{2,n} \\
&d_{3,1} \; d_{3,2} \; d_{3,3} \; \cdots \; d_{3,n} \\
&\vdots \\
&d_{n,1} \; d_{n,2} \; d_{n,3} \; \cdots \; d_{n,n}
\end{aligned}
$$
* $n$ 代表王老先生拥有的农场个数。
* $d_{i,j}$ 代表农场 $i$ 到 $j$ 的距离。
* 题目叙述中提到的 $m$ 并不会出现在输入中。
输出格式
$$D$$
* $D$ 为一正整数,代表王老先生从 $1$ 号农场出发、巡视经过所有他的农场、最后回到 $1$ 号农场的最短路径长度。
说明/提示
### 数据限制
* $2 \leq n\leq 5000$。
* $0\leq d_{i,j}\leq 10^8$。
* 若 $i\neq j$,则 $d_{i, j}> 0$。
* 若 $i = j$,则 $d_{i, j} = 0$。
* 对于所有 $i, j$,$d_{i, j} = d_{j, i}$。
* 保证存在一个正整数 $m\geq n$,满足存在一个 $m$ 点 $m-1$ 条边、每条边长度都大于零的连通图,满足 $d_{i, j}$ 为在其上取 $n$ 个点后的距离矩阵。
* 输入的数字皆为整数。
### 评分说明
本题共有六组子任务,条件限制如下所示。每一组可有一或多笔测试数据,该组所有测试数据皆需答对才会获得该组分数。
| 子任务 | 分数 | 额外输入限制 |
| :------: | :----: | ------------ |
| 1 | 7 | $n=3$。 |
| 2 | 12 | $n\leq 20$。 |
| 3 | 13 | $n\leq 200$ 且 $m=n$,也就是所有的农场都是王老先生的。 |
| 4 | 21 | $m=n$,也就是所有的农场都是王老先生的。 |
| 5 | 23 | $n\leq 1000$。 |
| 6 | 24 | 无额外限制。 |