P15360 「WYZOI R2」烟花

在春节期间，小 S 准备举办一场盛大的烟花表演。烟花的轨迹可以用一条折线 $L$ 表示，你已经知道折线 $L$ 可以由 $(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$ 这 $n$ 个点依次相连得到，保证 $x_1

**每个测试点包含多组测试数据**。输入的第一行包含一个正整数 $T$，表示测试数据的组数。对于每组测试数据： 第一行包含两个非负整数 $n,d$，分别表示点的数量与小 S 给出的参数。 第二行包含 $n$ 个非负整数 $x_1,x_2,\dots,x_n$，其中 $x_i$ 表示第 $i$ 个点的横坐标。 第三行包含 $n$ 个非负整数 $y_1,y_2,\dots,y_n$，其中 $y_i$ 表示第 $i$ 个点的纵坐标。

对于每组测试数据，输出一行一个整数，表示最多能删除的点数。

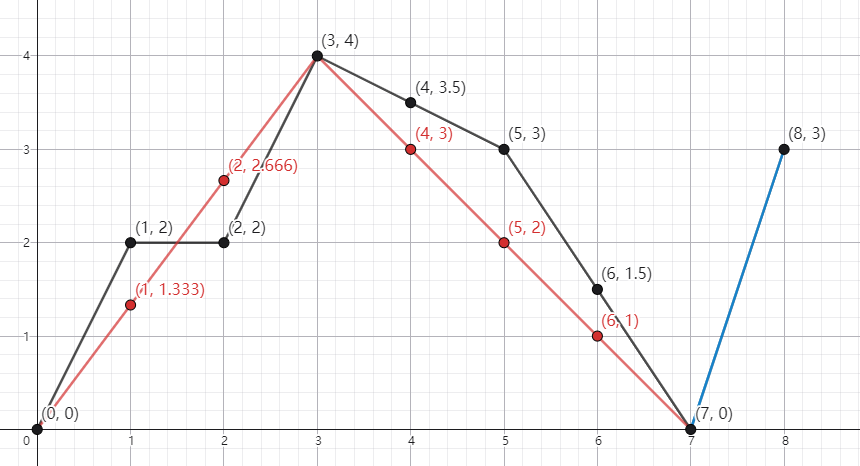
**【样例解释】**  对于第一组测试数据，一种合法的方案是删除点 $(1,2),(2,2),(5,3)$。图片中黑线为删除前的折线 $L$，红线为删除后的折线 $L'$，蓝线为 $L$ 与 $L'$ 的共同部分，每一个 $p$ 对应的点 $(p,L(p))$ 和 $(p,L'(p))$ 均在图中标出。 具体地，不同的 $p$ 对应的 $L(p)$ 及 $L'(p)$ 的值列表如下，不难验证 $|L(p)-L'(p)|$ 的值均不超过 $1$。 |$p=$|$0$|$1$|$2$|$3$|$4$|$5$|$6$|$7$|$8$| |:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:| |$L(p)=$|$0$|$2$|$2$|$4$|$\frac{7}{2}$|$3$|$\frac{3}{2}$|$0$|$3$| |$L'(p)=$|$0$|$\frac{4}{3}$|$\frac{8}{3}$|$4$|$3$|$2$|$1$|$0$|$3$| **【数据范围】** **本题采用捆绑测试。** | 子任务编号 | $n\le$ | 特殊性质 | 分值 | | :-----: | :---: | :--: | :--: | | $0$ | $15$ | $T\le 10,x_n\le 30$ | $15$ | | $1$ | $100$ | $T\le10,x_n\le 200$ | $20$ | | $2$ | $100$ | $T\le10$ | $20$ | | $3$ | $5000$ | $x_n\le 10^4$ | $20$ | | $4$ | $5000$ | 无 | $25$ | 对于 $100\%$ 的测试数据，保证：$1\le T\le 10^3$，$2 \le n \le 5 \times 10^3$，$0\le d,x_i,y_i \le 10^9$，$x_1