P1600 [NOIP 2016 Senior] Love Running Everyday

NOIP 2016 Senior D1T2.

Student Xiao C thinks running is very interesting, so he decides to make a game called "Love Running Everyday." "Love Running Everyday" is a nurturing-style game that requires players to log in on time every day to complete a check-in task. The map in this game can be viewed as a tree with $n$ nodes and $n-1$ edges. Each edge connects two nodes, and there exists exactly one path between any two nodes. The nodes on the tree are numbered with consecutive positive integers from $1$ to $n$. There are $m$ players. The $i$-th player starts at $s_i$ and ends at $t_i$. When the daily check-in task starts, all players simultaneously depart from their starting points at second $0$, moving at a speed of one edge per second, continuously along the shortest path toward their destination. Once a player reaches the destination, that player is considered to have completed the check-in task. (Since the map is a tree, each person's path is unique.) Xiao C wants to know the game's activity level, so an observer is placed at every node. The observer at node $j$ chooses to observe players at second $w_j$. A player can be observed by this observer if and only if the player also arrives at node $j$ exactly at second $w_j$. Xiao C wants to know how many players each observer will observe. Note: We assume that once a player reaches the destination, the player finishes the game and cannot wait to be observed later. That is, for a player whose destination is node $j$: if the player reaches the destination before second $w_j$, then the observer at node $j$ cannot observe that player; if the player arrives at the destination exactly at second $w_j$, then the observer at node $j$ can observe that player.

The first line contains two integers $n$ and $m$. Here $n$ is the number of nodes in the tree and also the number of observers, and $m$ is the number of players. Each of the next $n-1$ lines contains two integers $u$ and $v$, indicating that there is an edge between node $u$ and node $v$. The next line contains $n$ integers, where the $j$-th integer is $w_j$, meaning the observation time at node $j$. Each of the next $m$ lines contains two integers $s_i$ and $t_i$, representing a player's starting point and destination. For all testdata, it is guaranteed that $1 \leq s_i, t_i \leq n$, $0 \leq w_j \leq n$.

Output one line with $n$ integers. The $j$-th integer indicates how many players can be observed by the observer at node $j$.

Sample 1 Explanation. - For node $1$, $w_1 = 0$. Therefore, only players whose starting point is node $1$ will be observed. Players $1$ and $2$ are observed, for a total of $2$ players. - For node $2$, no player is at this node at second $2$, so $0$ players are observed. - For node $3$, no player is at this node at second $5$, so $0$ players are observed. - For node $4$, player $1$ is observed, so $1$ player is observed. - For node $5$, player $1$ is observed, so $1$ player is observed. - For node $6$, player $3$ is observed, so $1$ player is observed. Subtasks. The size and characteristics of each testpoint are as follows. Tip: The one's digit of the numbers in the constraints can help determine which type of data it is. | Testpoint ID | $n=$ | $m=$ | Convention | | :----------: | :--: | :--: | :--------: | | $1 \sim 2$ | $991$ | $991$ | All players' starting points equal their own destinations, i.e., $\forall i,\ s_i=t_i$. | | $3 \sim 4$ | $992$ | $992$ | All $w_j=0$. | | $5$ | $993$ | $993$ | None. | | $6 \sim 8$ | $99994$ | $99994$ | $\forall i \in [1,n-1]$, there is an edge between $i$ and $i+1$. That is, the tree degenerates into a chain $1,2,\dots,n$ connected in order. | | $9 \sim 12$ | $99995$ | $99995$ | All $s_i=1$. | | $13 \sim 16$ | $99996$ | $99996$ | All $t_i=1$. | | $17 \sim 19$ | $99997$ | $99997$ | None. | | $20$ | $299998$ | $299998$ | None. | Notes. (Tip: Because the original note is old, it may not fully reflect the current situation. We have made some updates to this note. The original text can be viewed on [this clipboard](https://www.luogu.com.cn/paste/3fneb8m6).) In the final evaluation, the stack size usage will not have a separate limit, but in our working environment there is a default limit of $1 \text{MiB}$. This may cause a stack overflow crash when the number of function calls is large. Deep recursion in your program often leads to this problem. If your program needs a large stack, please pay close attention to this issue. We can use some methods to change the stack size limit. - Linux We can enter the following command in the terminal: `ulimit -s 1048576`. This command changes the stack size limit to $1048576\text{KiB}=1 \text{GiB}$. For example, for the following program `sample.cpp`: ```cpp #include using namespace std; int f[1000005]; void dfs(int a){ if(a == 0){ f[a] = 0; return; } dfs(a - 1); f[a] = f[a - 1] + 1; } int main(){ dfs(1000000); return 0; } ``` Compile the above source code with `g++ sample.cpp -o sample` into the executable `sample`, and run it using `./sample`. If you run this program without using the command `ulimit -s 1048576`, `sample` will crash due to stack overflow; if you run it after using the above command, the program will not crash. In particular, when you open multiple terminals, they do not share this setting. You need to run the command in each of them. Please note that the stack usage is counted toward the total memory usage and is subject to the memory limit together with other parts of the program. 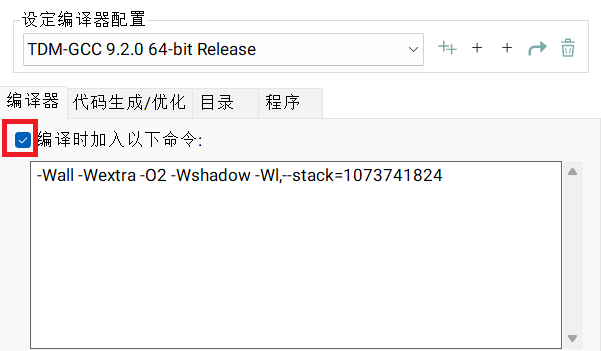- Windows If you are using Dev-C++ on Windows, select `Tools - Compiler Options` and fill in the following command in the area as shown: `-Wl,--stack=1073741824`. After filling it in, make sure the box “Add the following commands when compiling” is checked. Here, `1073741824` is in units of $\text{B/Bytes}$.   Translated by ChatGPT 5