P1661 Diffusion

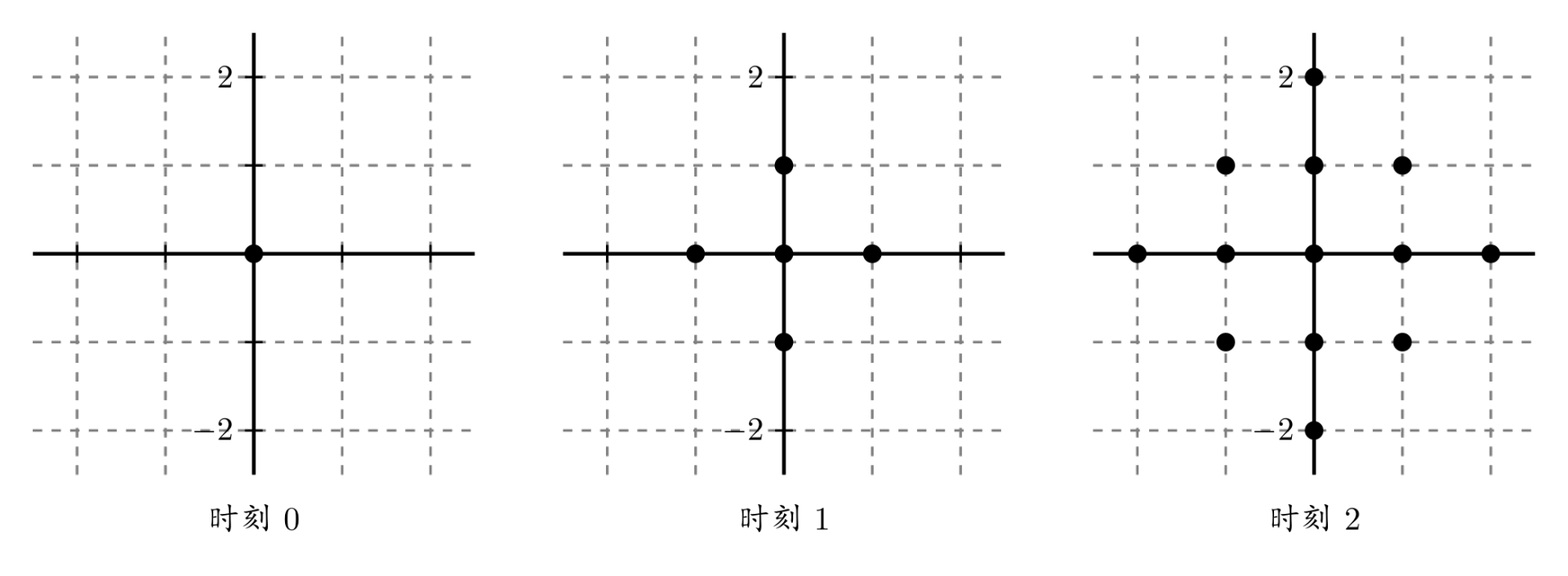
Each point expands by a distance of 1 in the four cardinal directions every unit of time, as shown in the figure.  Two points $a$ and $b$ are connected, denoted $e(a,b)$, if and only if the expansion regions of $a$ and $b$ have a nonempty intersection. A connected component is defined so that for any two points $u$ and $v$ within the component, there exists a path $e(u,a_0), e(a_0,a_1), \cdots, e(a_k,v)$. Given $n$ points on the plane, find the earliest time when they form a single connected component.

The first line contains an integer $n$. Each of the next $n$ lines contains two integers $X_i$ and $Y_i$, the coordinates of a point.

Output a single number, representing the earliest time when all points form a single connected component.

Constraints - For $20\%$ of the testdata, $1 \le n \le 5$, $1 \le X_i, Y_i \le 50$. - For $100\%$ of the testdata, $1 \le n \le 50$, $1 \le X_i, Y_i \le 10^9$. Translated by ChatGPT 5