P1756 [NOI2009] Outline

# Description Xiao Z is an outstanding mathematician. Being clever, he especially enjoys studying small mathematical problems. One day, he chose $n$ points on a sheet of paper and connected every pair with a pencil, forming $\dfrac{n(n-1)}{2}$ segments. Since the pencil is very thin, we can consider these segments to have width $0$. Looking at these segments, Xiao Z fell into deep thought. He believed some of these segments were more important and needed emphasis. So he took out a brush and restroked them. When the brush touches the paper, it forms a disk of radius $r$. While stroking a segment, the center of the brush (i.e., the center of the disk) starts from one endpoint and moves along the segment to the other endpoint. The figure below shows the result of emphasizing one segment in a configuration with $4$ points.  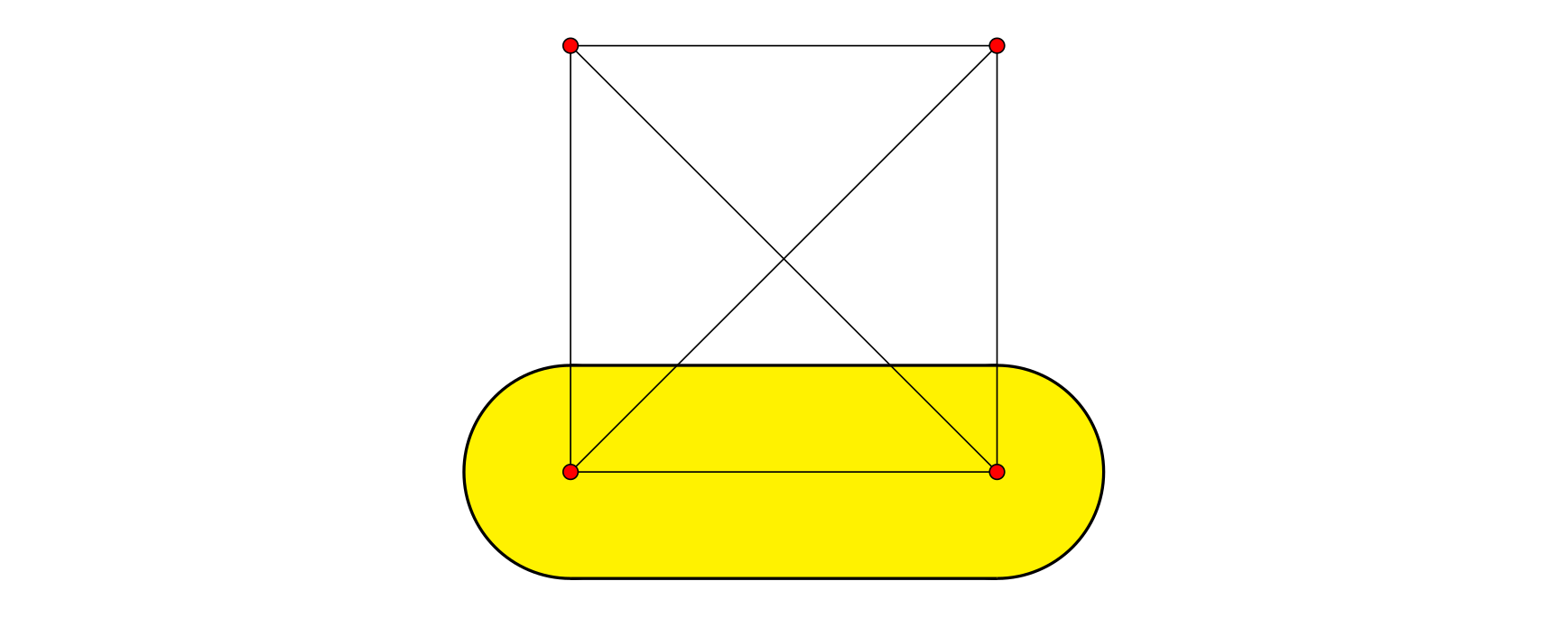Now, Xiao Z wants to know the total area on the paper that is emphasized after stroking. Can you help him answer this question?

小 Z 是一位杰出的数学家。聪明的他特别喜欢研究一些数学小问题。 有一天，他在一张纸上选择了 $n$ 个点，并用铅笔将它们两两连接起来，构成 $\dfrac{n(n-1)}{2}$ 条线段。由于铅笔很细，可以认为这些线段的宽度为 $0$。 望着这些线段，小 Z 陷入了冥想中。他认为这些线段中的一部分比较重要，需要进行强调。因此小 Z 拿出了毛笔，将它们重新进行了描边。毛笔画在纸上，会形成一个半径为 $r$ 的圆。在对一条线段进行描边时，毛笔的中心（即圆心）将从线段的一个端点开始，沿着该线段描向另一个端点。下图即为在一张 $4$ 个点的图中，对其中一条线段进行描边强调后的情况。  现在，小 Z 非常想知道在描边之后纸面上共有多大面积的区域被强调，你能帮助他解答这个问题么？

本题是一道提交答案型试题，所有的输入文件 `path1.in` $\sim$ `path10.in` 已在相应目录下。 输入文件请点击 [这里](http://pan.baidu.com/s/1gfeLZqz) 下载。 输入文件的第一行为一个正整数 $n$，表示选择的点的数目。 第二行至第 $n+1$ 行，其中：第 $i+1$ 行中为两个实数 $x_i,y_i$，表示点 $i$ 的坐标为 $(x_i,y_i)$。 第 $n+2$ 行为一个正整数 $m$，表示小 Z 认为比较重要的线段的条数。 第 $n+3$ 行至第 $n+m+2$ 行，每行有两个正整数 $a,b$，表示一条线段。其中 $a,b$ 两个数分别表示该线段的两个端点的编号。 第 $n+m+3$ 行中为一个实数 $r$，表示毛笔在纸上形成的圆的半径。 第 $n+m+4$ 行中为四个实数 $p_1,p_2,p_3,p_4$，即评分使用的参数。

The output file `path*.out` contains exactly one line with one number, which is the total area emphasized after stroking.

Each test point is scored independently. This problem has $4$ scoring parameters $p_1, p_2, p_3, p_4$ ($p_1 \lt p_2 \lt p_3 \lt p_4$), which are given in the input file. Your score will be determined by the following rules: - If your answer differs from the standard answer by no more than $p_1$, you will receive full score for that test point. - Otherwise, if your answer differs from the standard answer by no more than $p_2$, you will receive $70\%$ of the score for that test point. - Otherwise, if your answer differs from the standard answer by no more than $p_3$, you will receive $40\%$ of the score for that test point. - Otherwise, if your answer differs from the standard answer by no more than $p_4$, you will receive $10\%$ of the score for that test point. - Otherwise, your score for that test point will be $0$. Translated by ChatGPT 5