P1758 [NOI2009] Collecting Beads from Pipes

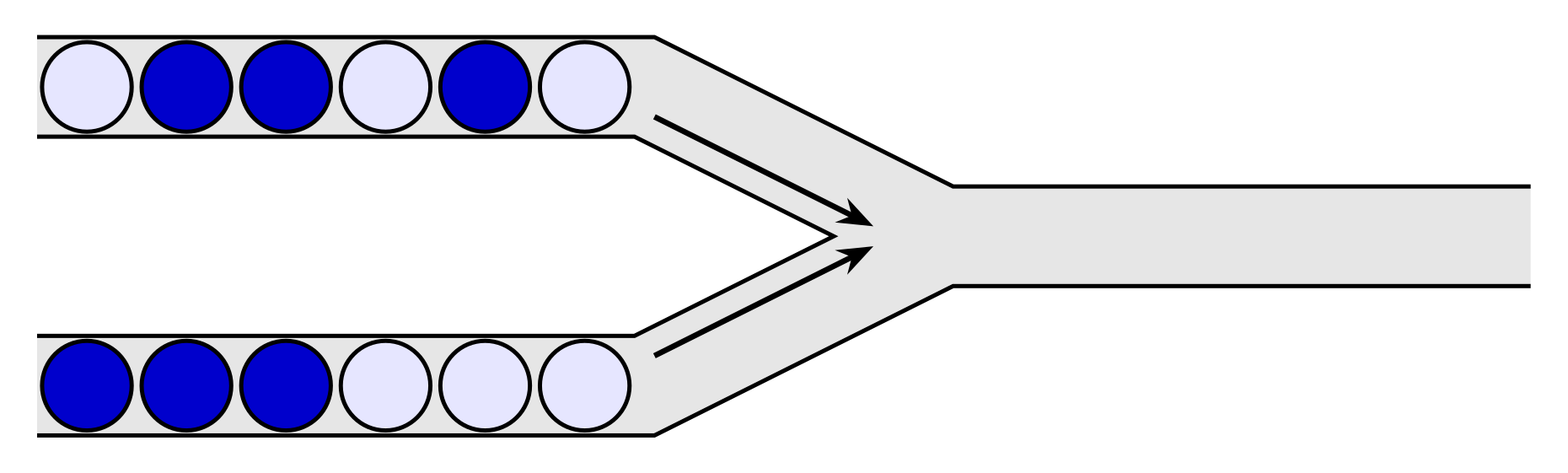
Collecting beads from pipes is a game that Little X likes very much. In this problem, we consider a simplified version of the game. The game screen is shown in Figure 1:  Initially, the upper and lower pipes on the left each contain some balls (there are two types: dark and light), and the output pipe on the right is empty. In each operation, you can choose one of the left pipes and push the rightmost ball in that pipe into the output pipe on the right. For example, if we first move one ball from the lower pipe to the output pipe, we get the situation shown in Figure 2.  Suppose there are $n$ balls in the upper pipe and $m$ balls in the lower pipe. Then the entire process requires $n+m$ operations, i.e., moving all balls from the left pipes into the output pipe. Finally, the $n+m$ balls form an output sequence in the output pipe from right to left. Math-loving Little X knows that there are $\dbinom{n+m}{m}$ different ways to operate, but different operation sequences may result in the same output sequence. For example, for the game situation shown in Figure 3:  We use A to denote light-colored balls and B to denote dark-colored balls. Let U denote moving the rightmost ball from the upper pipe, and D denote moving the rightmost ball from the lower pipe. Then there are $\binom{2+1}{1}=3$ different operation sequences: UUD, UDU, DUU. The resulting output sequences (from right to left) in the output pipe are BAB, BBA, and BBA, respectively. We can see that the last two operation sequences produce the same output sequence. Suppose there are $K$ different output sequences in total, and the $i$-th output sequence can be produced by $a_i$ different operation sequences. Clever Little X already knows that $$ \sum a_i=\binom{n+m}{m} $$ Therefore, Little X wants to compute $$ \sum a_i^2 $$ Can you help him compute this value? Since the value may be large, you only need to output the result modulo $1024523$.

The first line contains two integers $n,m$, the numbers of balls in the upper and lower pipes, respectively. The second line is a string of length $n$, representing the types of balls in the upper pipe from left to right. Here, A denotes a light-colored ball and B denotes a dark-colored ball. The third line is a string of length $m$, representing the types of balls in the lower pipe from left to right. It is guaranteed that both strings contain only the letters A and B.

Output a single integer, which is $\sum a_i^2$ modulo $1024523$.

Sample Explanation The sample corresponds to Figure 3. There are two different output sequences. The sequence BAB has $1$ way to produce it, and the sequence BBA has $2$ ways to produce it, so the answer is $5$. Constraints - For $30\%$ of the testdata, $m,n \leq 12$. - For $100\%$ of the testdata, $1 \leq m,n \leq 500$. Translated by ChatGPT 5