P1761 Square

There are $n$ squares of different sizes. Place them one by one, each rotated by $45$ degrees, in the first quadrant. Each square must have exactly one intersection point with the $x$-axis and must not overlap any previously placed squares. Subject to these conditions, the coordinate of the square’s intersection with the $x$-axis should be as small as possible. After all placements, when viewed from above, which squares are at least partially visible?

The input contains multiple test cases. For each test case, the first line contains an integer $n$, and the second line contains $n$ positive integers representing the side lengths of the squares. The input ends with a line containing a single $0$.

For each test case, output one line containing the indices of the squares that are at least partially visible, in increasing order and separated by spaces.

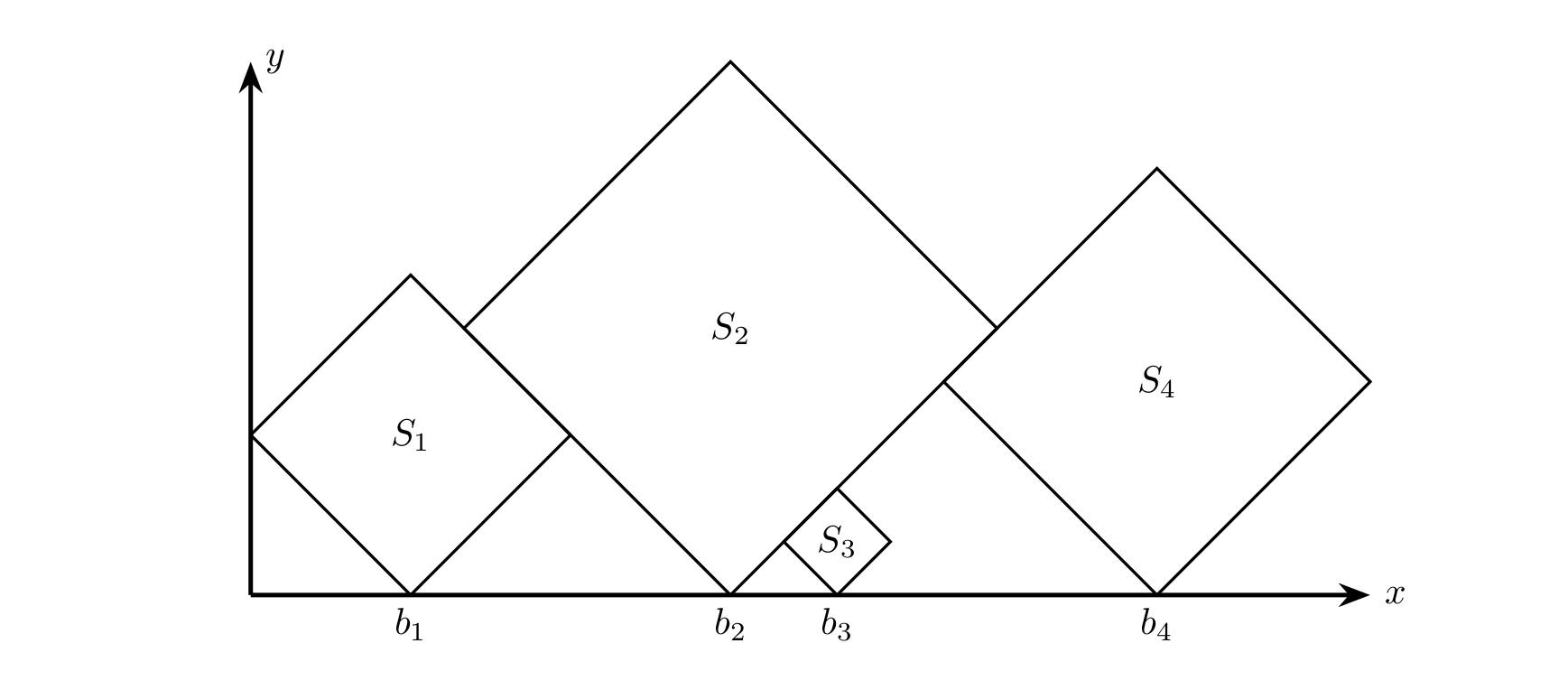
 ### Constraints - For $50\%$ of the testdata, $n \le 10$. - For $100\%$ of the testdata, $n \le 50$ and the sizes of the squares do not exceed $30$. Translated by ChatGPT 5