P1796 Thomas's Dream of Paradise

Thomas lives on a planet at level $0$. The environment there is extremely harsh: $12$ hours of work every day and piles of garbage are unbearable. He longs for the heavenly life on a planet at level $N$. There are flights that take people from a lower-level planet to a planet one level higher. Sometimes you need to pay a certain amount to the pilot, and sometimes you can receive some money. Thomas knows in advance all routes from the level $0$ planet to the level $N$ planet and the amount to pay (or receive) for each route. He wants to find a route with the lowest total price (or the highest total earnings).

- The first line contains a positive integer $N$ ($N \le 100$). The following data is divided into $N$ sections. In each section, the first line contains an integer $K_i$ ($K_i \le 100$), indicating that there are $K_i$ planets at level $i$. - In the next $K_i$ lines, the $j$-th line describes the planets at level $i - 1$ that are connected to the planet at level $i$ with index $j$, followed by the cost for each such flight (a positive number means paying, a negative number means earning; the absolute value does not exceed $1000$). Each line consists of several “index cost” pairs and ends with a single $0$. Each line contains at most $100$ routes.

Output the required (or obtained) total cost. A positive number means paying, and a negative number means earning.

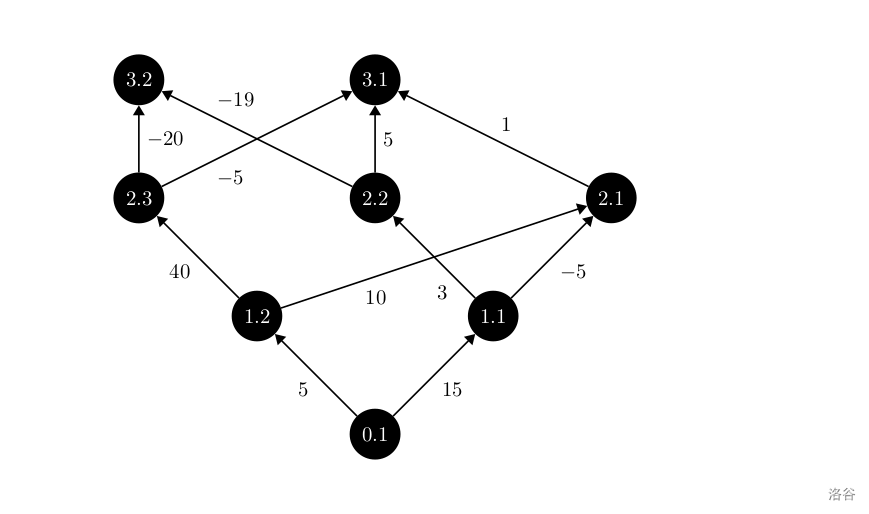
For $100\%$ of the testdata, $1 \le N \le 100$, $1 \le K_i \le 100$. Sample explanation:  Translated by ChatGPT 5