P1930 [USACO3.3] Camelot

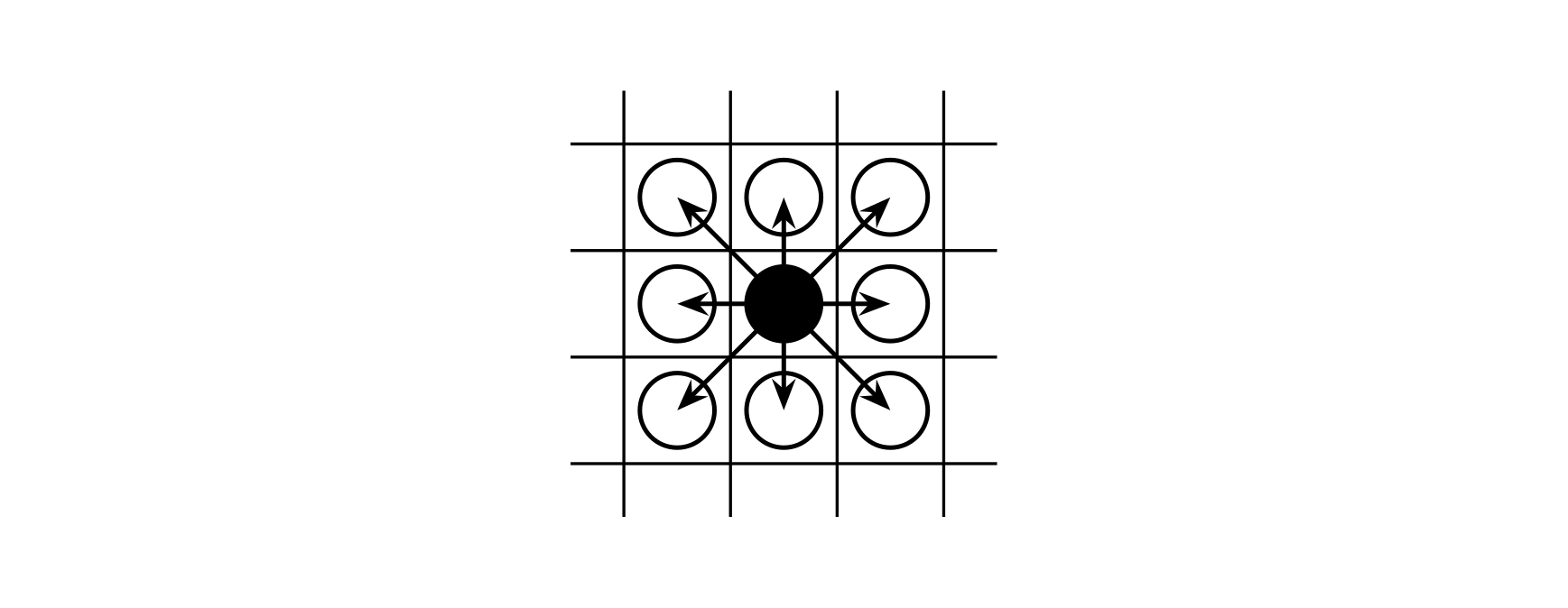
Long ago, King Arthur and his knights celebrated their friendship every New Year’s Day. To commemorate this, we treat these stories as a board game. A king and several knights are placed on a board consisting of many squares, with no two knights on the same square. This example uses the standard $8\times 8$ board.  The king can move to any adjacent square, from the black piece in the figure to any white piece, as long as he does not step off the board.  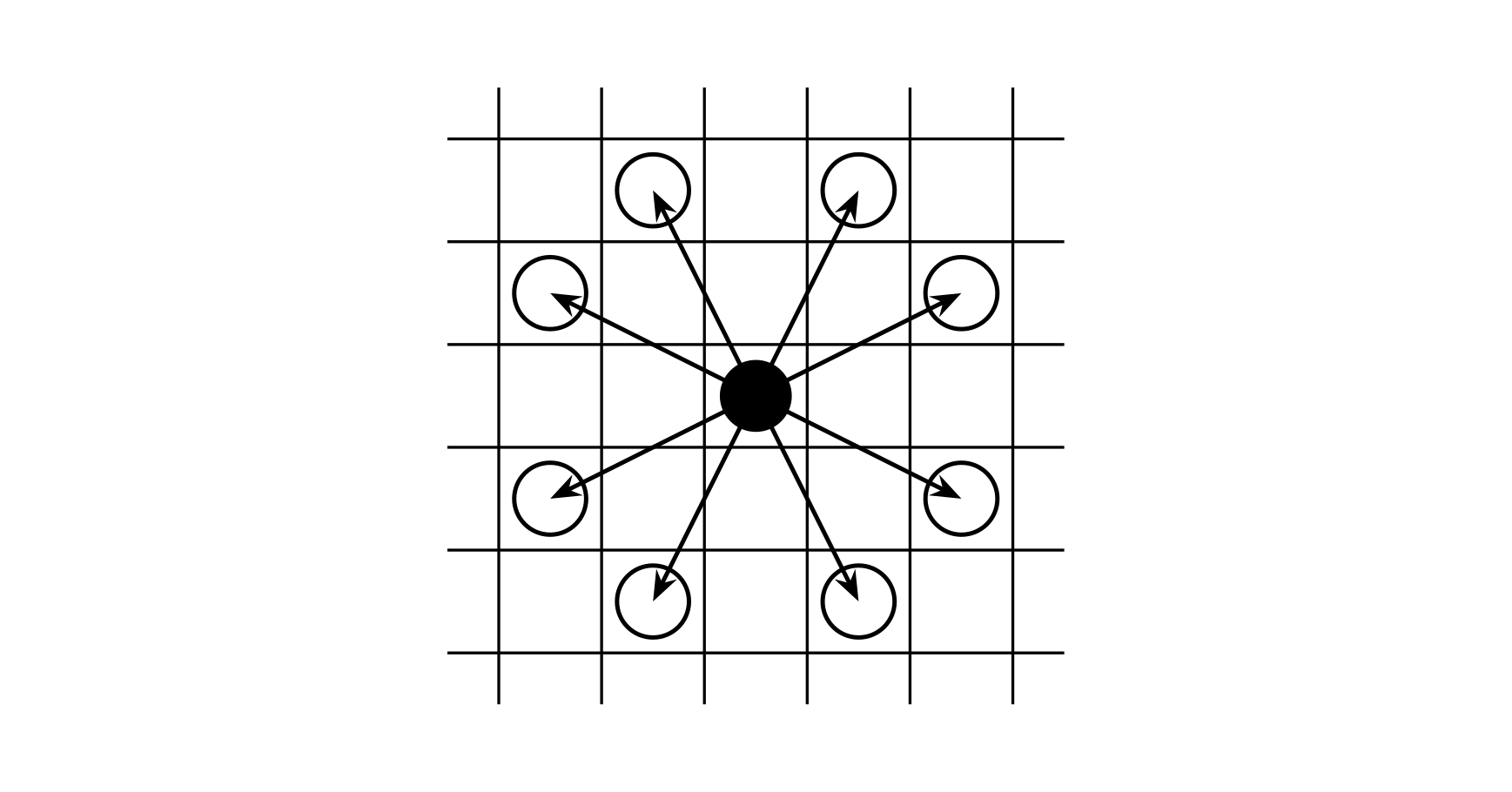A knight can move from the black piece in the figure to any white piece (in an L-shape), as long as it does not step off the board.  In this game, more than one piece may occupy the same square. Assume squares are large enough so that no piece blocks another’s movement. The task is to move all pieces onto a single square — using the minimum total number of moves. To achieve this, pieces must move according to the rules above. Additionally, the player may choose one knight to meet the king at some square; from that meeting point onward, the king and that knight move together using the knight’s movement rules. The other knights move independently to the gathering square. While the king and the chosen knight move together, only one piece’s move is counted per step. Compute the minimum number of moves needed to gather on a single square, and note that the player must also determine the gathering square. Of course, the pieces may gather anywhere on the board.

- The first line: two integers separated by a space, $R, C$, the number of rows and columns of the board. Columns do not exceed $26$, rows do not exceed $40$. - From the second line to the end: the input contains space-separated letter/number pairs, one or more per line. The first pair is the king’s position, followed by the knights’ positions. There may be no knights, or the entire board may be filled with knights. Rows are numbered starting from $1$, and columns are labeled starting from uppercase letter $A$.

Output a single line with the minimum number of moves required to gather all pieces on one square.

### Sample explanation They gather at $\tt B5$. - Knight $1$: $\tt A3\to B5$ (1 move). - Knight $2$: $\tt A8\to C7\to B5$ (2 moves). - Knight $3$: $\tt H1\to G3\to F5\to D4$, the king meets this knight here, $\to \tt B5$ (4 moves). - Knight $4$: $\tt H8\to F7\to D6\to B5$ (3 moves). $1+2+4+3=10$ moves. Problem translation from NOCOW. USACO Training Section 3.3. Translated by ChatGPT 5