P1945 Boundless Grid

In a table with $R$ rows and $C$ columns, each cell is a square. Such a table is called a "grid", and the four vertices of each cell are called "lattice points". A square whose four vertices all lie on lattice points is called a "lattice square"; similarly, an equilateral triangle whose three vertices all lie on lattice points is called a "lattice equilateral triangle". For given positive integers $R$ and $C$ ($R,C \le 10$), please compute the numbers of lattice squares and lattice equilateral triangles in the grid. GZH has seen this kind of problem many times on math exams. After some daydreaming, he thinks it is akin to classic problem types such as grid problems, counting problems, and symmetry problems, and can be solved quickly. However, he also finds that once $R$ and $C$ no longer satisfy the condition in the statement and become very large, the counting becomes tedious. Of course, you will be delighted by this, because programming can help here again. Can you write a program to help GZH complete this tedious counting on this boundless grid?

One line containing $2$ positive integers $R$ and $C$ separated by a single space.

One line containing $2$ integers $\mathit{ans}_1$ and $\mathit{ans}_2$ separated by a single space, representing in order the numbers of lattice squares and lattice equilateral triangles in the grid.

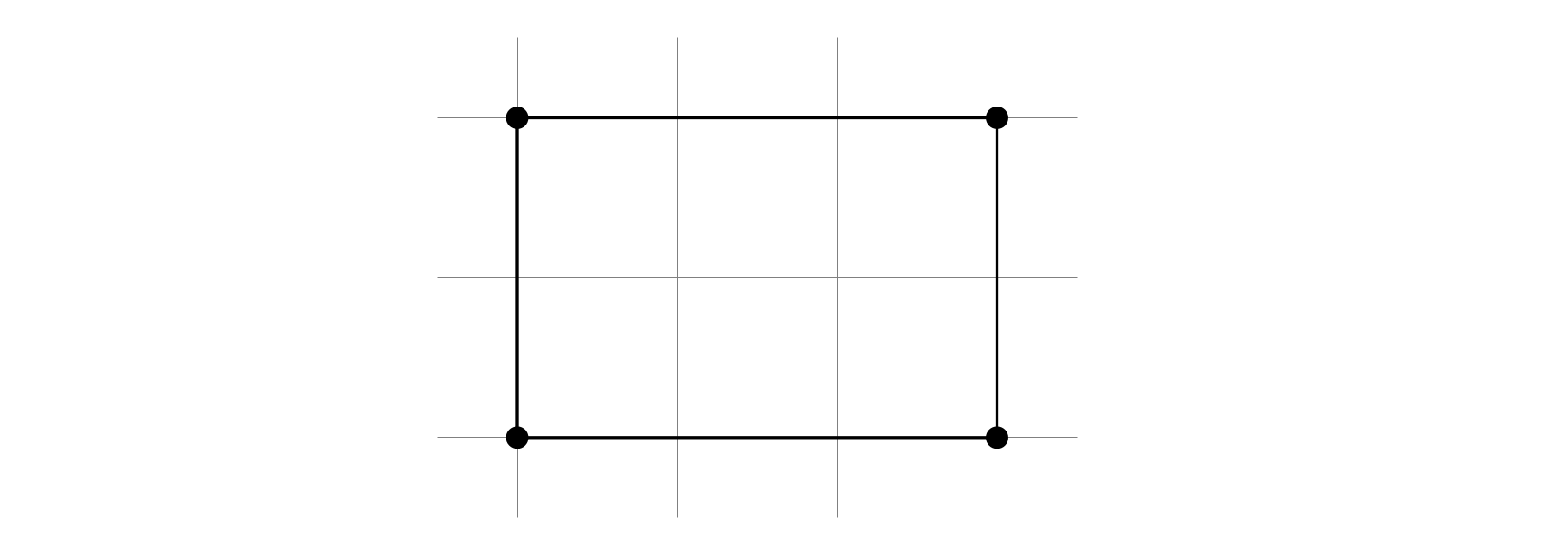
### Sample Explanation  The input asks for the numbers of lattice squares and lattice equilateral triangles in the figure. - The number of lattice squares is counted as follows:  There are ten in total. - It is not hard to see that no lattice equilateral triangle can be found in the given grid. ### Constraints and Notes - For $30\%$ of the testdata, $R,C \le 50$. - For $50\%$ of the testdata, $R,C \le 10^3$. - For $70\%$ of the testdata, $R,C \le 10^5$, $\mathit{ans}_1,\mathit{ans}_2