P1971 [NOI2011] Tutu and Dandan's Game

These days, Tutu and Dandan have taken a liking to a new board game. The game is played on an $n$-by-$m$ board. Before the game starts, exactly one cell on the board is empty, and every other cell contains a piece that is either black or white. In each game, Tutu always moves first, and then the two players alternate. The moves are defined as follows: - On Tutu’s turn, she chooses a white piece adjacent to the empty cell and moves it into the empty cell. - On Dandan’s turn, he chooses a black piece adjacent to the empty cell and moves it into the empty cell. The first player who cannot move according to the rules loses the game. For convenience, the operation “move the piece in row $x$, column $y$ into the empty cell” is denoted by $M(x,y)$. For example, here are three sample games.    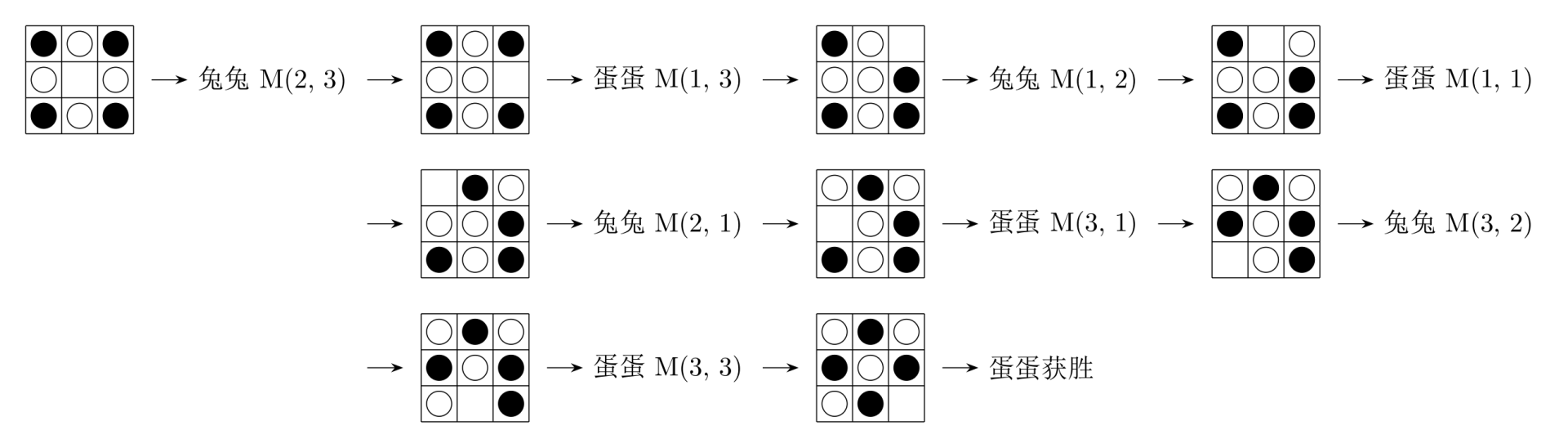Recently Tutu keeps losing, and Dandan is especially smug about it, so Tutu asks her good friend—you—for help. She brings you the full move log of a game she lost to Dandan. Please point out every move where she “made a mistake” in that game. Note: - Two cells are adjacent if and only if they share a common side. - Tutu’s move is a “mistake” if and only if, before the move Tutu had a winning strategy, and after the move Dandan has a winning strategy.

The first line contains two positive integers $n, m$. The next $n$ lines describe the initial board. The $i$-th of these lines contains $m$ characters. Each character is one of the uppercase letters `X`, `O`, or the dot `.`. They denote a black piece, a white piece, and an empty cell, respectively. The dot `.` appears exactly once. The next line contains an integer $k$ ($1 \leq k \leq 1000$), indicating that Tutu and Dandan each made $k$ moves. The next $2k$ lines describe the game. The $(2i - 1)$-th line is Tutu’s $i$-th move (the move with index $i$), and the $2i$-th line is Dandan’s $i$-th move. Each move is described by two integers $x, y$, meaning the piece at row $x$, column $y$ is moved into the empty cell. The input guarantees that there is exactly one empty cell on the board; every move made by Tutu and Dandan is legal; and Dandan wins in the end.

The first line contains an integer $r$, the total number of mistakes made by Tutu. Then output $r$ lines in increasing order, giving the indices of Tutu’s “mistaken” moves. The $i$-th of these lines contains an integer $a_i$, meaning that Tutu’s $i$-th mistake is her $a_i$-th move in the game.

For $100\%$ of the testdata, $1 \leq n \leq 40$, $1 \leq m \leq 40$, $1 \leq k \leq 1000$. ::cute-table{tuack} | Test point ID | $n$ | $m$ | |:-:|:-:|:-:| | $1,2$ | $n=1$ | $1\leq m\leq 20$ | | $3$ | $n=3$ | $m=4$ | | $4,5$ | $n=4$ | $m=4$ | | $6,7$ | $n=4$ | $m=5$ | | $8$ | $n=3$ | $m=7$ | | $9\sim 14$ | $n=2$ | $1\leq m\leq 40$ | | $15,16$ | $1\leq n\leq 16$ | $1\leq m\leq 16$ | | $17\sim 20$ | $1\leq n\leq 40$ | $1\leq m\leq 40$ | Translated by ChatGPT 5