P1974 Gene Aggregation

German scientists have always been amazed by the resistance of African wild monkeys, because they found that without medical conditions, African wild monkeys get sick less often than all other wild animals. Recent studies have made new discoveries: Dr. Smith found a rare antibody in African wild monkeys and suspects that it is this rare antibody that helps them resist invading viruses. Dr. Smith immediately started studying this antibody. In the initial observations, Dr. Smith found nothing special and thought it very simple, because each gene group of the antibody contains only one pair of "primitives" (Dr. Smith considers a gene group to consist of several pairs of primitives). But when Dr. Smith implanted the virus into the culture medium containing the antibody, a miracle happened! Those simple genomes kept aggregating (each time two genomes merged into a new genome), and eventually all genomes merged into a very large genome. It is precisely this large genome, having aggregated the advantages of all original genomes, that can slowly and individually consume the viruses implanted in the culture medium. Below is the approximate process of primitive aggregation in antibody genomes observed by Dr. 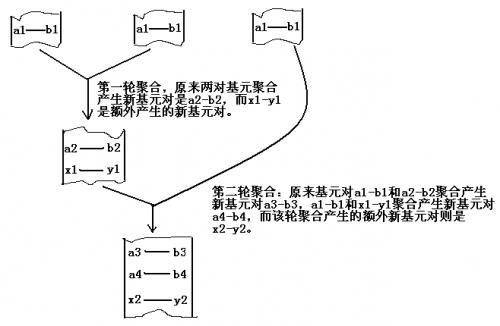Smith under a high-power microscope:  Through further observation and research, Dr. Smith found that the antibody genes seem to always follow a certain method during aggregation, which ensures that the final genome has the maximum number of primitive pairs (each primitive pair produces $1$ unit of bioenergy). After each merge of two genomes, the total number of primitive pairs in the new genome is the sum of the following two parts: 1. Every time two genomes merge, an additional, unknown primitive pair is produced. 2. When two genomes merge, each primitive pair in one genome merges with each primitive pair in the other genome to produce a new primitive pair. Dr. Smith also found that at any moment only two genomes merge, that is, the merges happen sequentially, not simultaneously. Although he observed the aggregation principle, even with the initial number of genomes known, Dr. Smith still could not compute the total energy of the final large genome produced by aggregation. Now he asks you to write a program to compute it.

You are given $n$ cards, each with the number $1$, and a machine. You will perform the following operation $n-1$ times: put two cards into the machine and obtain a new card with the number $xy+1$, where $x, y$ are the numbers on the two cards you put in. Question: After performing $n-1$ operations, what is the maximum possible number on the remaining card?

One line containing a single positive integer $n$ ($1 \le n \le 10^4$).

One line containing a single positive integer representing the answer.

Translated by ChatGPT 5