P1979 [NOIP 2013 Senior] Huarong Dao

NOIP 2013 Senior D2T3.

`小 B` recently got hooked on the Huarong Dao sliding puzzle, but it always takes him a long time to finish one game. So he thought of writing a program to solve it: given a board position, determine whether the puzzle is impossible to finish, and if it can be finished, what is the minimum time required. The Huarong Dao that `小 B` plays is slightly different from the classic one. The rules are: 1. On an $ n \times m $ board there are $ n \times m $ cells. Exactly one cell is empty, and each of the remaining $ n \times m - 1 $ cells has one piece on it. Every piece is of size $ 1 \times 1 $. 2. Some pieces are fixed, while others are movable. 3. Any piece on a cell adjacent to the empty cell (sharing a side) can move into the empty cell. The goal is to move a specified movable piece from its start position to a target position. Given a board, the game can be played $ q $ times. The fixed cells on the board never change, but the initial position of the empty cell, the specified movable piece’s start position, and its target position may differ each time. In the $ i $-th play, the empty cell is at row $ EX_i $, column $ EY_i $, the specified movable piece starts at row $ SX_i $, column $ SY_i $, and its target is row $ TX_i $, column $ TY_i $. Assume `小 B` can perform one piece-move per second, and all other operations take negligible time. For each game, tell `小 B` the minimum time required, or tell him that the game cannot be completed.

The first line contains $ 3 $ integers, separated by a single space, which are $ n, m, q $. The next $ n $ lines describe an $ n \times m $ board. Each line contains $ m $ integers separated by single spaces. Each integer describes the state of a cell: $ 0 $ means the piece on that cell is fixed, and $ 1 $ means the piece on that cell is movable or the cell is empty. The next $ q $ lines each contain $ 6 $ integers $ EX_i, EY_i, SX_i, SY_i, TX_i, TY_i $, separated by single spaces, giving the empty cell’s position, the specified piece’s start position, and its target position for each game.

Output $ q $ lines. Each line contains $ 1 $ integer, the minimum time required for that game, or $ -1 $ if the target cannot be achieved.

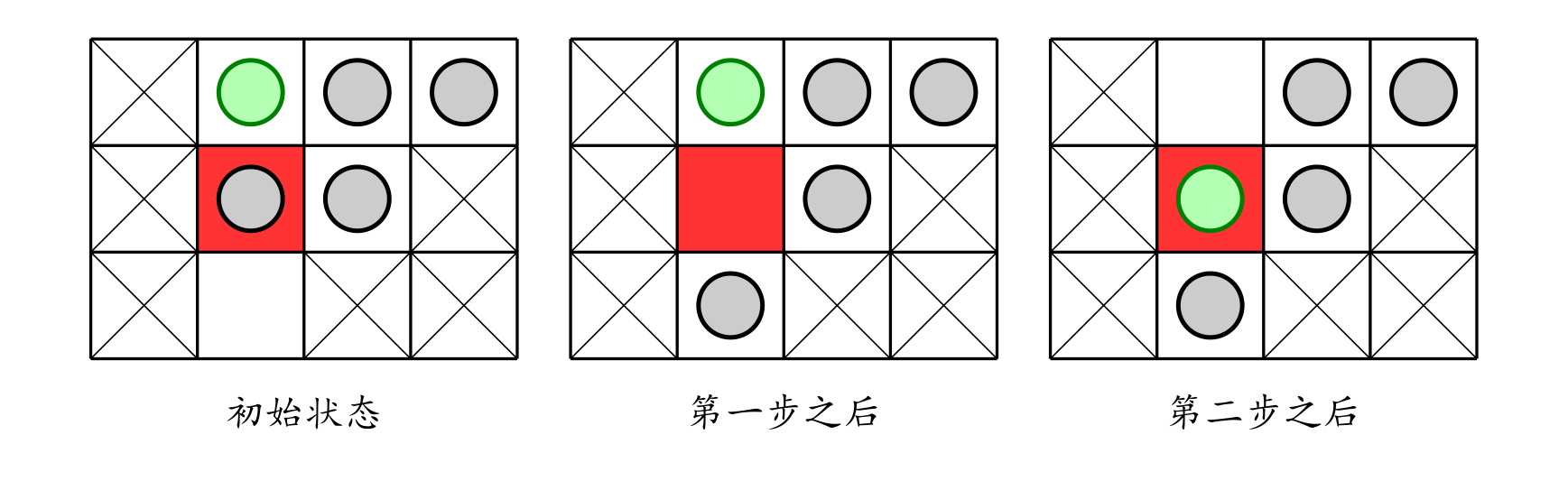
Explanation of the sample I/O: Cells with an X are fixed, the red cell is the target position, and circles denote pieces; the green circle is the target piece. 1. In the first game, the empty cell starts at $ (3, 2) $ (as shown), and the goal is to move the piece initially at $ (1, 2) $ (the green circle) to the target position $ (2, 2) $ (the red cell). The moves are as follows:  2. In the second game, the empty cell starts at $ (1, 2) $ (as shown), and the goal is to move the piece initially at $ (2, 2) $ (the green circle) to the target position $ (3, 2) $.  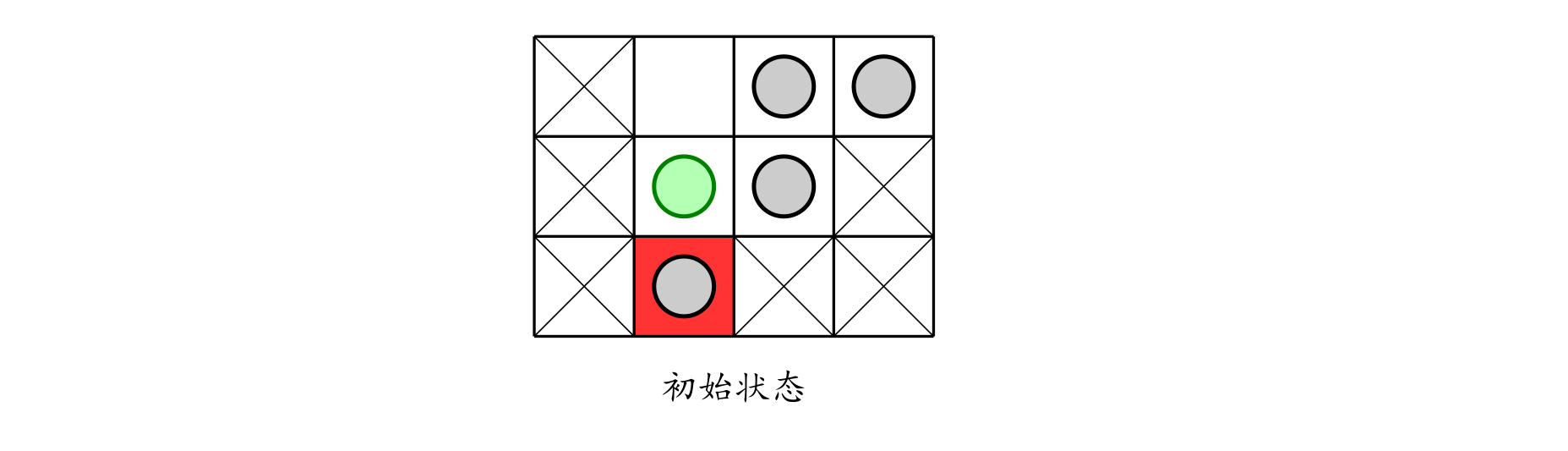To move the target piece into the target cell, the empty cell must first enter the target cell. For the empty cell to enter the target cell, it must swap with the piece currently on $ (2, 2) $. After that, the only piece that can swap with the empty cell is that same piece on the target cell, so the target piece can never reach its target. The game is impossible. Constraints - For $ 30\% $ of the testdata, $ 1 \le n, m \le 10, q = 1 $. - For $ 60\% $ of the testdata, $ 1 \le n, m \le 30, q \le 10 $. - For $ 100\% $ of the testdata, $ 1 \le n, m \le 30, q \le 500 $. Translated by ChatGPT 5