P1983 [NOIP 2013 Junior] Station Classification

NOIP 2013 Junior T4.

Along a one-way railway line, there are $n$ stations numbered $1, 2, \dots, n$ in order. Each station has a level, with the minimum level being $1$. There are several train services operating on this line, and each service satisfies the following rule: if the service stops at station $x$, then among the stations between its origin and terminal station, every station whose level is greater than or equal to the level of station $x$ must also be a stop. Note: The origin and terminal stations are, of course, also counted as known stops. For example, the table below shows the operation of $5$ services. Among them, the first $4$ services satisfy the rule, while the $5$-th service does not, because it stops at station $3$ (level $2$) but skips station $6$ (also level $2$) along the route.  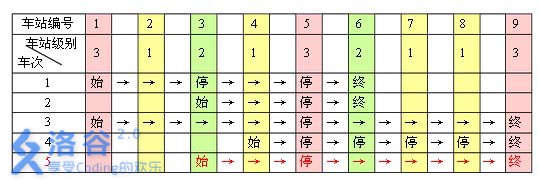Given the operation of $m$ services (all of which satisfy the rule), determine the minimum number of distinct levels needed for these $n$ stations.

The first line contains $2$ positive integers $n, m$, separated by a space. On line $i + 1$ for $1 \le i \le m$, first there is a positive integer $s_i$ ($2 \le s_i \le n$), indicating that the $i$-th service has $s_i$ stops; then follow $s_i$ positive integers, the indices of all stops, in increasing order. Each pair of numbers is separated by a single space. The input guarantees that all services satisfy the rule.

Output a single integer, the minimum number of levels into which the $n$ stations can be partitioned.

For $20\%$ of the testdata, $1 \le n, m \le 10$. For $50\%$ of the testdata, $1 \le n, m \le 100$. For $100\%$ of the testdata, $1 \le n, m \le 1000$. Translated by ChatGPT 5