P2009 Running

Running is an interesting sport, especially because it can develop one’s mind. Chang Sheniu (pinyin) loves running.

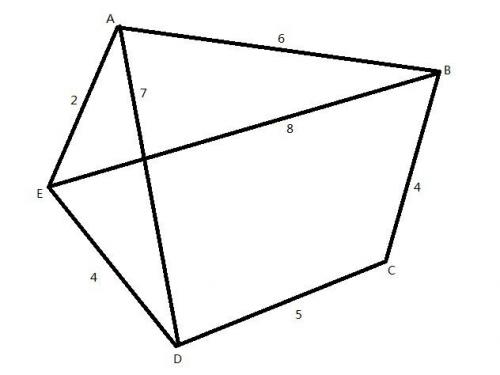
Chang Sheniu’s running field is a polygon (number of sides $\leq 20$, each vertex is denoted by an uppercase English letter). Inside the polygon, there are also some trails that connect two non-adjacent vertices. All edges and trails are bidirectional. For example, in the figure below:  Suppose Chang Sheniu runs from $A$ to $D$, the shortest path is $A-E-D$ (length $6$). You are given the number of sides $n$, the length of each polygon edge, the number of internal connections $k$, the two endpoints and the length of each internal connection, and the start and end vertices. Please output the length of the shortest path. However, Chang Sheniu has a bit of OCD: if there are multiple roads directly connecting the same pair of vertices, he will choose the longest one. Note: The input does not guarantee that the start and end vertices are different, nor that the endpoints of an internal trail are different. When reading the input, if there are multiple internal trails between two vertices, the distance between them is the maximum of those trails. Therefore, if an internal trail starts and ends at the same vertex, the distance from that vertex to itself is not $0$. # Description

- The first line contains $2$ numbers, $n, k$. - The second line contains $n$ numbers, giving the lengths of the polygon’s edges in clockwise order, i.e., the lengths of $AB, BC, CD, DE, \ldots$. - Each of the following $k$ lines contains two letters and a number. The two letters are the endpoints of an internal connection, and the number is its length. - The last line contains two letters, the start and end vertices of the run. Within each line, letters and numbers are separated by a single space.

One line with one number: the length of the shortest path.

- For $20\%$ of the testdata, $k = 0$. - For $50\%$ of the testdata, $k \leq 10$. - For $100\%$ of the testdata, $1 \leq n \leq 20$, $0 \leq k \leq 100$, and all path lengths do not exceed $1000$. Translated by ChatGPT 5