P2011 Compute Voltage

I believe many of you easily beat problems 1 and 2 (jǔruò, please ignore this line). I also believe everyone is very interested in physics (crowd: we are also very interested in punching people). So here are another 100 points for the "Physicalers."

You are given a resistor network. The resistance on each edge is known, and the voltages between several nodes and the negative terminal are given (the power-supply voltage is constant). Now compute the voltage between any two nodes.

The first line contains four positive integers $n, m, k, q$, indicating there are $n$ nodes (some nodes may be connected by wires and thus are equivalent to one node; nodes are numbered $1$ to $n$, and node $0$ is the negative terminal of the power supply), $m$ fixed resistors (each fixed resistor connects two nodes), the positive terminal of the power supply has $k$ terminals, and there are $q$ queries. The next $k$ lines each contain two positive integers, indicating the index of this positive terminal and the voltage $u_i$ between this binding post and the negative terminal. The next $m$ lines each contain three positive integers $v_i, w_i, r_i$, indicating that there is a resistor of resistance $r_i$ between nodes $v_i$ and $w_i$. The next $q$ lines each contain two positive integers $a_i, b_i$, indicating that you need to compute the voltage between $a_i$ and $b_i$.

Output $q$ lines. Each line contains one real number representing the voltage between $a_i$ and $b_i$ (rounded to two decimal places). If the voltage at $a_i$ is less than the voltage at $b_i$, output a negative value.

Constraints - For $10\%$ of the testdata, $1 \le q \le 10$. - For $20\%$ of the testdata, $1 \le n \le 10$, and the circuit is guaranteed to be series, parallel, or a mixed connection. - For $40\%$ of the testdata, $1 \le n \le 40$, $k \le 5$. - For $100\%$ of the testdata, $1 \le k \le n \le 200$, $1 \le m \le 2 \times 10^5$, $1 \le r_i, u_i \le 10^4$, $1 \le q \le 10^6$. Time and Memory Limits Time limit: 1.00 s, Memory limit: 125.00 MB. Sample Explanation As shown in the figure.  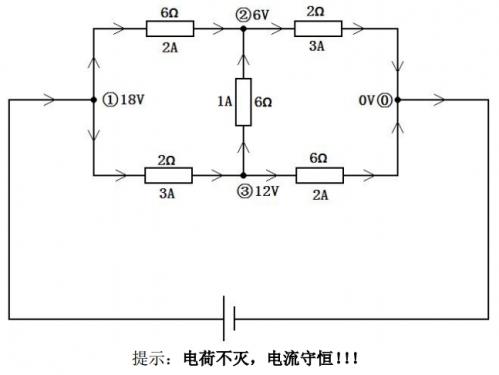Translated by ChatGPT 5