P2046 [NOI2010] Elevation

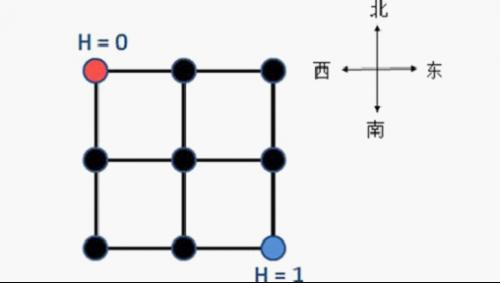
YT City is a well-planned city divided by the main east–west and north–south roads into $n \times n$ regions. For simplicity, you can regard YT City as a square, and each region as a square as well. Thus, the city contains $(n+1) \times (n+1)$ intersections and $2n \times (n+1)$ bidirectional roads (simply called roads), where each bidirectional road connects two adjacent intersections on the main roads. The figure below shows a map of YT City when $n = 2$, where the city is divided into $2 \times 2$ regions, containing $3 \times 3$ intersections and $12$ bidirectional roads.  Xiao Z, the mayor of the city, obtained the bidirectional traffic flow for each road in both directions during the morning rush hour, i.e., the number of people passing along that direction during the rush hour. Each intersection has an elevation value. YT City residents consider uphill walking tiring: ascending by a height of $h$ consumes $h$ stamina. Going downhill costs no stamina. Therefore, if the endpoint elevation minus the start elevation of a road is $h$ (note that $h$ may be negative), then the stamina consumed by a person traversing that road is $\max\{0, h\}$. Xiao Z also measured that the intersection at the northwest corner has elevation $0$, and the intersection at the southeast corner has elevation $1$ (as shown above), but the elevations of the other intersections are unknown. He wants to know, in the most favorable situation (i.e., you may assign elevations to the other intersections arbitrarily), the minimum possible total stamina spent on climbing by everyone during the morning rush hour.

The first line contains an integer $n$. Then follow $4n(n + 1)$ lines, each containing a non-negative integer representing the traffic flow for one road in one direction. Input order: first $n(n + 1)$ numbers for all movements from West to East, then $n(n + 1)$ numbers for all movements from North to South, then $n(n + 1)$ numbers for all movements from East to West, and finally $n(n + 1)$ numbers for all movements from South to North. For each direction, the entries are listed by starting intersections ordered from North to South, and when the north–south position is the same, from West to East (see the sample input).

Output a single number, the minimum possible total stamina spent on climbing by everyone during the morning rush hour in the most favorable situation, rounded to the nearest integer.

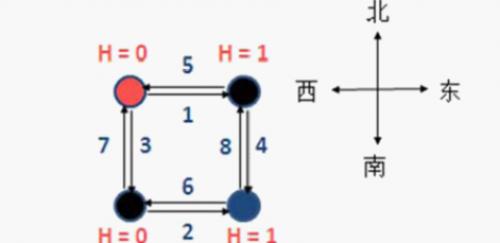
 # Constraints - For $20\%$ of the testdata: $n \leq 3$. - For $50\%$ of the testdata: $n \leq 15$. - For $80\%$ of the testdata: $n \leq 40$. - For $100\%$ of the testdata: $1 \leq n \leq 500$, $0 \leq \text{flow} \leq 10^6$, and all flows are integers. Translated by ChatGPT 5