P2047 [NOI2007] Social Network

In the study of social networks (Social Network), we often use graph theory to explain social phenomena. Consider the following problem: There are $n$ people in a social circle, and the relationships between people have different strengths. We model this relationship network as an undirected graph with $n$ nodes. If two different people know each other, we connect an undirected edge between their corresponding nodes and assign it a positive weight $c$. The smaller $c$ is, the closer their relationship is. We measure the closeness between two people $s$ and $t$ by the length of the shortest path between their corresponding nodes. Note that other nodes on a shortest path provide some convenience for the connection between $s$ and $t$, that is, these nodes have a certain degree of importance for the connection between $s$ and $t$. We can measure a node’s importance in the social network by counting the number of shortest paths that pass through a node $v$. Considering that there may be multiple shortest paths between two nodes $A$ and $B$, we modify the definition of importance as follows: let $C_{s,t}$ denote the number of different shortest paths from $s$ to $t$, and let $C_{s,t}(v)$ denote the number of shortest paths from $s$ to $t$ that pass through $v$. Then define: $$ I(v)=\sum_{s \ne v,t\ne v} \frac{C_{s,t}(v)}{C_{s,t}}$$ as the importance of node $v$ in the social network. To make $I(v)$ and $C_{s,t}(v)$ meaningful, we stipulate that the social networks to be processed are connected undirected graphs, i.e., there is a shortest path of finite length between any two nodes. Given such a weighted undirected graph describing a social network, please compute the importance of each node. Constraints: - For $50\%$ of the testdata, $n \le 10, m \le 45$. - For $100\%$ of the testdata, $n \le 100, m \le 4500$, each edge weight $c$ is a positive integer and $1 \leqslant c \leqslant 1000$. - The graph is guaranteed to be connected, and the number of shortest paths between any two nodes does not exceed $10^{10}$.

The first line contains two integers $n$ and $m$, the number of nodes and undirected edges in the social network. In the undirected graph, all nodes are numbered from $1$ to $n$. Each of the next $m$ lines contains three integers $a, b, c$ describing an undirected edge connecting nodes $a$ and $b$ with weight $c$. Note that there is at most one undirected edge between any two nodes, and there are no self-loops in the undirected graph (that is, there is no undirected edge whose two endpoints are the same node).

Output $n$ lines, each containing a real number rounded to $3$ decimal places. The real number on the $i$-th line represents the importance of node $i$ in the social network.

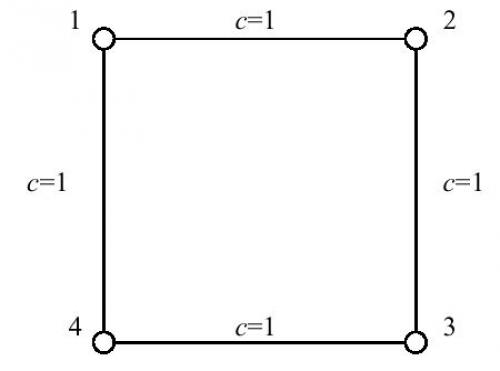
 For node $1$, only the shortest paths from node $2$ to node $4$ and from node $4$ to node $2$ pass through node $1$. Moreover, there are $2$ shortest paths between node $2$ and node $4$. Therefore, by the definition, the importance of node $1$ is $\frac{1}{2}+\frac{1}{2}=1$. Due to the symmetry of the graph, the importance of the other three nodes is also $1$. Translated by ChatGPT 5